题目内容
等腰三角形的两边分别为5和8，那么它的周长是（ ）
| A、13 | B、18 |
| C、21 | D、18或21 |
考点：等腰三角形的性质,三角形三边关系
专题：
分析：分腰长为5和8两种情况讨论，再利用三角形三边关系进行验证，再求其周长．
解答：解：
当腰长为5时，三角形的三边分别为5、5、8，满足三角形的三边关系，此时其周长为5+5+8=18；
当腰长为8时，三角形的三边分别为8、8、5，满足三角形的三边关系，此时其周长为8+8+5=21；
综上可知该三角形的周长为18或21，
故选D．
当腰长为5时，三角形的三边分别为5、5、8，满足三角形的三边关系，此时其周长为5+5+8=18；
当腰长为8时，三角形的三边分别为8、8、5，满足三角形的三边关系，此时其周长为8+8+5=21；
综上可知该三角形的周长为18或21，
故选D．
点评：本题主要考查等腰三角形的性质，掌握等腰三角形的两腰相等是解题的关键，注意分两种情况并利用三角形的三边关系进行验证．
练习册系列答案
名校课堂系列答案
相关题目
如图所示：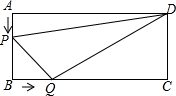
如图，在矩形ABCD中，AB=6cm，BC=12cm，点P点P从A出发沿边AB以1cm/s的速度向点B移动；同时，点Q从点B出发沿边BC以2cm/s的速度向点C移动，（P、Q两点同时停止运动）几秒钟后△PBQ的面积等于28cm2？