题目内容
如图，P是半径为2的⊙O外一点，PB是⊙O的切线，B为切点，弦BC∥OA，且BC=2，求图中阴影部分面积．考点：切线的性质,扇形面积的计算
专题：
分析：首先证明△OAB为等边三角形，然后证明S△OCB=S△PCB，问题即可解决．
解答：
解：如图，连接OA、OB；
∵OA=OB=OC，
∴△OAB为等边三角形，
∴∠CBO=60°，而BC∥OA，
∴S△OCB=S△PCB，
∴S阴影=S扇形OBC；
∵S扇形OBC=
=
，
∴图中阴影部分面积为
．
解：如图，连接OA、OB；∵OA=OB=OC，
∴△OAB为等边三角形，
∴∠CBO=60°，而BC∥OA，
∴S△OCB=S△PCB，
∴S阴影=S扇形OBC；
∵S扇形OBC=
| 60π×22 |
| 360 |
| 2π |
| 3 |
∴图中阴影部分面积为
| 2π |
| 3 |
点评：该题以圆为载体，以扇形面积计算的考查为核心构造而成；同时还渗透了对三角形面积等积变换等的考查．
练习册系列答案
相关题目
如图，P是Rt△ABC的斜边BC上异于B、C的一点，过点P作直线截△ABC，使截得的三角形与△ABC相似，满足这样条件的直线共有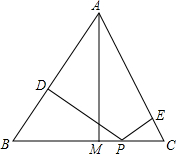
如图，已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为h1、h2、h3，△ABC的高为h，请探究图中的h1、h2、h3、h的关系．
如图所示：
如图，在△ABC中，CF：EF：BE=3：2：1，BD：AD=2：3．求CH：HG：DG的比．