题目内容
如图，直角梯形ABCD中，AD=3，AB=11，BC=6，AB⊥BC，动点P在线段AB上运动，如果满足△ADP和△BCP相似，计算此时线段AP的长度．考点：相似三角形的性质,直角梯形
专题：分类讨论
分析：分△ADP∽△DPC和△ADP∽△BCP两种情况进行讨论，利用相似三角形的对应边的比相等即可求解．
解答：解：①当△ADP∽△DPC时，
有
=
=
AP=2或9；
②当△ADP∽△BCP时，
=
，
=
，
解得：AP=
，
综上知：AP=2或9或
有
| AD |
| BP |
| AP |
| BC |
| 3 |
| 11-AP |
| AP |
| 6 |
AP=2或9；
②当△ADP∽△BCP时，
| AD |
| BC |
| AP |
| BP |
| 3 |
| 6 |
| AP |
| 11-AP |
解得：AP=
| 11 |
| 3 |
综上知：AP=2或9或
| 11 |
| 3 |
点评：本题考查了相似三角形的性质，相似三角形的对应边的比相等，分两种情况进行讨论是关键．
练习册系列答案
相关题目
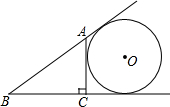如图，AC⊥BC于点C，⊙O与直线AB、BC、CA都相切，若⊙O的半径等于1，BC=2，△ABC的周长是
在Rt△ABC中，∠C=90°．