题目内容
17．
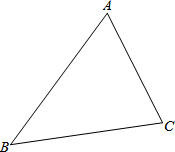在一个住宅小区里，有一块三角形绿地，现准备在其中建一个圆形花坛，使它面积最大．请你在图中画出这个圆形花坛的位置．结论：三角形内切圆面积最大．
分析 由题意知，这个面积最大的花坛是△ABC的内切圆，画出它的内切圆即可．
解答 
解：作∠ABC的平分线BD，
作∠ACB的角的平分线CE，BD与CE交于点F，
作FG⊥BC，垂足为F，以点F为圆心，FG为半径作圆F，
则圆F是所求的面积最大的圆．
故答案为：三角形内切圆面积最大．
点评 本题考查了角平分线的作法和角平分线的性质：角平分线的交点到各边的距离相等，这样以角平分线交点为圆心，到各边的距离为半径做圆，此圆为三角形的内切圆，面积最大．
练习册系列答案
相关题目
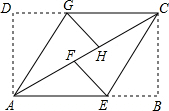如图，ABCD是矩形纸片，翻折∠B、∠D，使BC，AD恰好落在AC上，设F，H分别是B，D落在AC上的两点．E、G分别是折痕CE、AG与AB、CD的交点．连接GF、HE，若AB=4cm，BC=3cm，则四边形GFEH的面积等于$\frac{3}{2}$cm2．
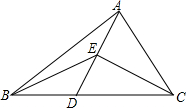如图，点D在△ABC的边BC上，连接AD，在线段AD上任取一点E（点E不与点A、D重合）
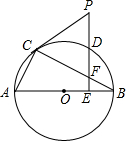如图，Rt△ABC内接于⊙O，D为BC中点，过点D作DE⊥AB于E，交BC于F，交过点C作⊙O的切线于点P．
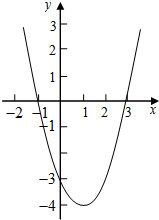阅读材料，解答问题．