题目内容
12.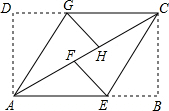 如图,ABCD是矩形纸片,翻折∠B、∠D,使BC,AD恰好落在AC上,设F,H分别是B,D落在AC上的两点.E、G分别是折痕CE、AG与AB、CD的交点.连接GF、HE,若AB=4cm,BC=3cm,则四边形GFEH的面积等于$\frac{3}{2}$cm2.
如图,ABCD是矩形纸片,翻折∠B、∠D,使BC,AD恰好落在AC上,设F,H分别是B,D落在AC上的两点.E、G分别是折痕CE、AG与AB、CD的交点.连接GF、HE,若AB=4cm,BC=3cm,则四边形GFEH的面积等于$\frac{3}{2}$cm2.
分析 利用翻折变换的性质得出DG=GH,HE=BE,∠GHA=∠CFE=90°,AD=AH=CF=BC=3cm,进而得出HC的长,再利用勾股定理得出GH的长,进而得出答案.
解答 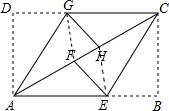 解:连接GF和HE,
解:连接GF和HE,
∵ABCD是矩形纸片,翻折∠B、∠D,使BC,AD恰好落在AC上,设F,H分别是B,D落在AC上的两点,
∴DG=GH,HE=BE,∠GHA=∠CFE=90°,AD=AH=CF=BC=3cm,
∴FH=1cm,HC=2cm,
设DG=GH=x,则GC=4-x,
∴GH2+HC2=GC2,
则x2+22=(4-x)2,
解得:x=$\frac{3}{2}$,
同理可得:EF=$\frac{3}{2}$,
则四边形GFEH的面积为:1×$\frac{3}{2}$=$\frac{3}{2}$(cm2).
故答案为:$\frac{3}{2}$cm2.
点评 此题主要考查了翻折变换的性质以及勾股定理等知识,得出HC的长是解题关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
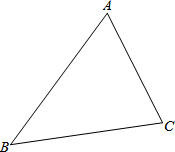
13. 如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )
如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )
 如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )
如图,将三角形ABC沿BC方向平移2cm得到三角形DEF,若三角形ABC的周长为16cm,则四边形ABFD的周长为( )| A. | 22cm | B. | 20cm | C. | 18cm | D. | 16cm |
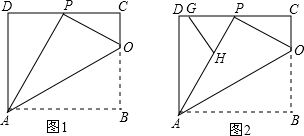
 在一个住宅小区里,有一块三角形绿地,现准备在其中建一个圆形花坛,使它面积最大.请你在图中画出这个圆形花坛的位置.
在一个住宅小区里,有一块三角形绿地,现准备在其中建一个圆形花坛,使它面积最大.请你在图中画出这个圆形花坛的位置. 如图,已知在?ABCD中,延长AD到E,使DE=AD,延长AB到F,使BF=AB,分别以AF、AE为斜边作Rt△ANF,Rt△AME,且∠F=∠E.求证:CM=CN.
如图,已知在?ABCD中,延长AD到E,使DE=AD,延长AB到F,使BF=AB,分别以AF、AE为斜边作Rt△ANF,Rt△AME,且∠F=∠E.求证:CM=CN.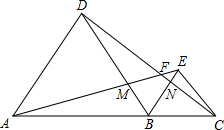 如图,A、B、C三点在同一条直线上,△ABD、△BCE为等边三角形,(等边三角形的三边相等,三个内角都是60°).
如图,A、B、C三点在同一条直线上,△ABD、△BCE为等边三角形,(等边三角形的三边相等,三个内角都是60°).