题目内容
9.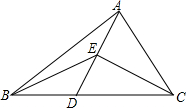 如图,点D在△ABC的边BC上,连接AD,在线段AD上任取一点E(点E不与点A、D重合)
如图,点D在△ABC的边BC上,连接AD,在线段AD上任取一点E(点E不与点A、D重合)(1)猜想:∠BEC与∠ABE、∠ACE、∠BAC有什么数量关系?并证明你的猜想
(2)若点E在AD所在的直线上移动,且点E不与点A、D重合,请画图探究∠BEC与∠ABE、∠ACE、∠BAC之间的数量关系,写出关系式,并选择一个加以证明.
分析 (1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BED=∠ABE+∠BAD,∠CED=∠ACE+∠CAD,再根据∠BAD+∠CAD=∠BAC证明;
(2)分点E在BC的下方时,利用四边形的内角和定理解答;点B在BC的上方时,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAD=∠ABE+∠AEB,∠CAD=∠ACE+∠AEC,再根据∠AEB+∠AEC=∠BEC解答.
解答 (1)∠BEC=∠ABE+∠ACE+∠BAC;
证明:由三角形的外角性质得,∠BED=∠ABE+∠BAD,∠CED=∠ACE+∠CAD,
∵∠BAD+∠CAD=∠BAC,
∴∠BEC=∠BED+∠CED=∠ABE+∠BAD+∠ACE+∠CAD=∠ABE+∠ACE+∠BAC,
即:∠BEC=∠ABE+∠ACE+∠BAC;
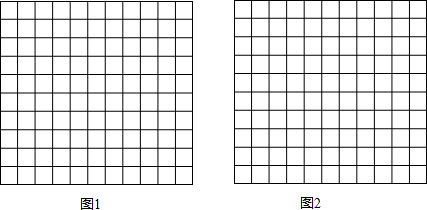
(2)解:如图1,点E在BC的下方时,
由四边形的内角和定理得,∠BEC+∠ABE+∠ACE+∠BAC=360°;
如图2,点B在BC的上方时,
由三角形的内角和定理得,∠BAD=∠ABE+∠AEB,∠CAD=∠ACE+∠AEC,
∵∠AEB+∠AEC=∠BEC,
∴∠BAC=∠ABE+∠ACE+∠BEC.
点评 本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,熟记性质是解题的关键,难点在于(2)分情况讨论,作出图形更形象直观.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 已知在Rt△ABC中,AC>BC,∠ACB=90°,点D是AB边的中点,过点D作DE⊥AB于点D,交∠ACB的角平分线于点E,连接AE,BE.证明:AE=EB,并且AE⊥EB.
已知在Rt△ABC中,AC>BC,∠ACB=90°,点D是AB边的中点,过点D作DE⊥AB于点D,交∠ACB的角平分线于点E,连接AE,BE.证明:AE=EB,并且AE⊥EB.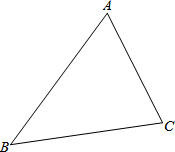 在一个住宅小区里,有一块三角形绿地,现准备在其中建一个圆形花坛,使它面积最大.请你在图中画出这个圆形花坛的位置.
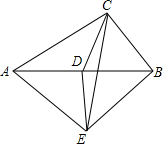
在一个住宅小区里,有一块三角形绿地,现准备在其中建一个圆形花坛,使它面积最大.请你在图中画出这个圆形花坛的位置. 如图,已知在?ABCD中,延长AD到E,使DE=AD,延长AB到F,使BF=AB,分别以AF、AE为斜边作Rt△ANF,Rt△AME,且∠F=∠E.求证:CM=CN.
如图,已知在?ABCD中,延长AD到E,使DE=AD,延长AB到F,使BF=AB,分别以AF、AE为斜边作Rt△ANF,Rt△AME,且∠F=∠E.求证:CM=CN. 如图所示,有五个大小相同的正方形拼成“T“字形,试将它分成四块全等的图形.
如图所示,有五个大小相同的正方形拼成“T“字形,试将它分成四块全等的图形.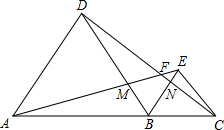 如图,A、B、C三点在同一条直线上,△ABD、△BCE为等边三角形,(等边三角形的三边相等,三个内角都是60°).
如图,A、B、C三点在同一条直线上,△ABD、△BCE为等边三角形,(等边三角形的三边相等,三个内角都是60°).