题目内容
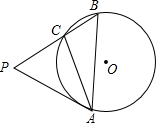 如图,在△ABC中,∠BAC=30°,∠ABC=45°,BC=1,⊙O是△ABC的外接圆,过点A作⊙O的切线,交BC的延长线于点P.
如图,在△ABC中,∠BAC=30°,∠ABC=45°,BC=1,⊙O是△ABC的外接圆,过点A作⊙O的切线,交BC的延长线于点P.(1)求⊙O的半径长;
(2)求∠P的度数.
考点:切线的性质
专题:计算题
分析:(1)连结OC、OA、OC,如图,根据圆周角定理得∠AOC=2∠ABC=90°,则△OAC为等腰直角三角形,所以OC=
AC=1;
(2)连结OB,如图,先判断△OBC为等边三角形,则∠BOC=60°,根据圆周角定理得∠BAC=
∠BOC=30°,再根据切线的性质得∠OAP=90°,则可计算出∠PAC=90°-∠OAC=45°,所以∠BAP=∠BAC+∠PAC=75°,然后利用三角形内角和计算∠P的度数.
| ||
| 2 |
(2)连结OB,如图,先判断△OBC为等边三角形,则∠BOC=60°,根据圆周角定理得∠BAC=
| 1 |
| 2 |
解答:解:(1)连结OC、OA、OC,如图,
∵∠ABC=45°,
∴∠AOC=2∠ABC=90°,
∴△OAC为等腰直角三角形,
∴OC=
AC=
•
=1,
即⊙O的半径长;
(2)连结OB,如图,
∵OB=OC=1,
而BC=1,
∴OB=BC=OC,
∴△OBC为等边三角形,
∴∠BOC=60°,
∴∠BAC=
∠BOC=30°,
∵PA为⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∴∠PAC=90°-∠OAC=90°-45°=45°,
∴∠BAP=∠BAC+∠PAC=30°+45°=75°,
∴∠P=180°-∠BAP-∠ABP=180°-75°-45°=60°.

∵∠ABC=45°,
∴∠AOC=2∠ABC=90°,
∴△OAC为等腰直角三角形,
∴OC=
| ||
| 2 |
| ||
| 2 |
| 2 |
即⊙O的半径长;
(2)连结OB,如图,
∵OB=OC=1,
而BC=1,
∴OB=BC=OC,
∴△OBC为等边三角形,
∴∠BOC=60°,
∴∠BAC=
| 1 |
| 2 |
∵PA为⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∴∠PAC=90°-∠OAC=90°-45°=45°,
∴∠BAP=∠BAC+∠PAC=30°+45°=75°,
∴∠P=180°-∠BAP-∠ABP=180°-75°-45°=60°.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理.

练习册系列答案
相关题目
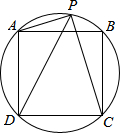 正方形ABCD的四点在☉O上,若P是弧AB上一点,请确定PA+PC与PD之间的数量关系,并证明你的结论.
正方形ABCD的四点在☉O上,若P是弧AB上一点,请确定PA+PC与PD之间的数量关系,并证明你的结论. (1)⊙O的直径为11cm,若圆心到一直线的距离为5.5cm,那么这条直线和圆的关系是
(1)⊙O的直径为11cm,若圆心到一直线的距离为5.5cm,那么这条直线和圆的关系是
 如图,等边△ABC的边长为10,BD⊥AC于点D,点M在AB上,AM=4,在BD上找一点P,使PN+PA最小,求这个最小值.
如图,等边△ABC的边长为10,BD⊥AC于点D,点M在AB上,AM=4,在BD上找一点P,使PN+PA最小,求这个最小值.