Question

19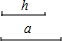．如图，已知线段a，h．
（1）作等腰△ABC，使底边BC=a，BC边上的高为h．要求用尺规作图，写出作法，保留作图痕迹．
（2）在（1）中，若BC=30，BC边上高为8，求AB的长．

Answer 1

分析 （1）分别以B、C为圆心，大于$\frac{1}{2}$BC为半径画弧，分别相交，作出BC的垂直平分线，再以D为圆心h长为半径画弧，交垂直平分线于点A，连接AB、AC即可；
（2）直接利用等腰三角形的性质得出BD的长，再利用勾股定理得出答案．

解答 解：（1）如图所示：①作射线BF，在射线上截取BC=a；
②分别以B、C为圆心，大于$\frac{1}{2}$BC为半径画弧，分别相交，作出BC的垂直平分线EF；
③以D为圆心h长为半径画弧，交垂直平分线于点A，
则△ABC即为所求；

（2）由题意可得：BD=DC=$\frac{1}{2}$BC=15，
AD=8，
则AB=$\sqrt{1{5}^{2}+{8}^{2}}$=17．

点评 本题考查了复杂作图以及画线段的垂直平分线、在直线上截取线段、等腰三角形的性质，正确掌握基本作图方法是解题关键．