题目内容
4. 如图,正方形PQMN和正方形MABC中,点N在CM上,QM=2,AM=6,D是PB的中点,那么DM的长是2$\sqrt{5}$.
如图,正方形PQMN和正方形MABC中,点N在CM上,QM=2,AM=6,D是PB的中点,那么DM的长是2$\sqrt{5}$.
分析 连接PM、BM,根据正方形的性质求出PM、BM,并判断出△PMB是直角三角形,再利用勾股定理列式求出PB,然后根据直角三角形斜边上的中线等于斜边的一半解答即可.
解答 解:如图, 连接PM、BM,
连接PM、BM,
在正方形PQMN和正方形MABC中,PM=$\sqrt{2}$QM=2$\sqrt{2}$,BM=$\sqrt{2}$AM=6$\sqrt{2}$,∠PMN=∠CMB=45°,
∴∠PMB=45°+45°=90°,
∴△PMB是直角三角形,
由勾股定理得,PB=$\sqrt{P{M}^{2}+B{M}^{2}}$=4$\sqrt{5}$,
∵D是PB的中点,
∴DM=$\frac{1}{2}$PB=2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,正方形的性质,勾股定理,难点在于作辅助线构造出直角三角形.

练习册系列答案
相关题目
15. 如图所示是一个几何体,其左视图是( )
如图所示是一个几何体,其左视图是( )
 如图所示是一个几何体,其左视图是( )
如图所示是一个几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图所示,在?ABCD中,BC=2AB,点M是AD的中点,CE⊥AB于E,
如图所示,在?ABCD中,BC=2AB,点M是AD的中点,CE⊥AB于E,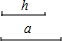 如图,已知线段a,h.
如图,已知线段a,h. 如图,AB∥EF,∠1=60°,∠2=120°,试说明CD∥EF.
如图,AB∥EF,∠1=60°,∠2=120°,试说明CD∥EF. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回,点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回,点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0). 如图,AB∥CD∥EF,∠B=70°,∠E=140°,则∠BCE=30°.
如图,AB∥CD∥EF,∠B=70°,∠E=140°,则∠BCE=30°.