题目内容
14．一列火车身长160米，它以每秒16米的速度向前行驶，与此同时，在铁轨旁边有一条与铁轨平行的人行道，火车头位置对应于人行道B处，一个人在B点前方400米的A处，以每秒1.5米的速度迎着火车的方向走来，问：经过几秒钟后车尾从人的旁边经过？分析 根据题意结合火车长加400=人与火车行驶的总距离进而得出等式求出答案．
解答 解：经过x秒钟后车尾从人的旁边经过，根据题意可得：
（16+1.5）x=160+400，
解得：x=32．
答：经过32秒钟后车尾从人的旁边经过．
点评 此题主要考查了一元一次方程的应用，根据题意表示出人与火车行驶的总距离是解题关键．
练习册系列答案
相关题目
4．已知A（$\sqrt{2}$，1）是正比例函数图象上一点，此函数图形与x轴正半轴夹角α的cosα的值为（ ）
| A． | $\sqrt{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
6．已知a=$\sqrt{2}$，b=$\sqrt{5}$，则$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}÷\frac{1}{a}$的值为（ ）
| A． | $\sqrt{5}-\sqrt{2}$ | B． | 3 | C． | $\sqrt{2}+\sqrt{5}$ | D． | $\sqrt{2}-\sqrt{5}$ |
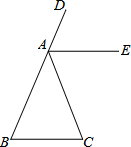如图，已知∠DAC是△ABC的一个外角，请在下列三个关系：