题目内容
一组数据x1,x2,x3,x4,x5的平均数是4,方差是3,那么另一组数据2x1-3,2x2-3,2x3-3,2x4-3,2x5-3的平均数和方差分别是 .
考点:方差,算术平均数
专题:计算题
分析:根据方差和平均数的变化规律可得:数据2x1-3,2x2-3,2x3-3,2x4-3,2x5-3的平均数是2×4-3,方差是3×22,再进行计算即可.
解答:解:∵数据x1,x2,x3,x4,x5的平均数是4,
∴另一组数据2x1-3,2x2-3,2x3-3,2x4-3,2x5-3的平均数是2×4-3=5;
∵数据x1,x2,x3,x4,x5的方差是3,
∴另一组数据2x1,2x2,2x3,2x4,2x5的方差是3×22=12,
∴另一组数据2x1-3,2x2-3,2x3-3,2x4-3,2x5-3的方差是12;
故答案为:5,12.
∴另一组数据2x1-3,2x2-3,2x3-3,2x4-3,2x5-3的平均数是2×4-3=5;
∵数据x1,x2,x3,x4,x5的方差是3,
∴另一组数据2x1,2x2,2x3,2x4,2x5的方差是3×22=12,
∴另一组数据2x1-3,2x2-3,2x3-3,2x4-3,2x5-3的方差是12;
故答案为:5,12.
点评:本题考查了方差和平均数:关键是掌握方差和平均数的变化规律;一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
相关题目
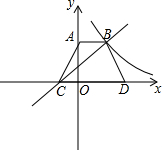 如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数
如图,等腰梯形ABCD中,AB∥CD,AB=2,CD=4,A(0,3),直线y=ax+b过B、C两点,反比例函数