题目内容
 如图,已知A(-4,O),B(2,0),点C在直线y=-
如图,已知A(-4,O),B(2,0),点C在直线y=-| 1 |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
考点:一次函数综合题
专题:
分析:根据∠A为直角,∠B为直角与∠C为直角三种情况进行分析.
解答: 解:由题意知,直线y=-
解:由题意知,直线y=-
x+2与x轴的交点为(4,0),与y轴的交点为(0,2),如图:
当∠A为直角时,过点A作垂线与直线的交点W(-4,4),
当∠A为直角时,过点B作垂线与直线的交点S(2,1),
当∠C为直角时,过AB中点E(-1,0),作垂线与直线的交点为F(-1,2.5),则EF=2.5<3,
所以以3为半径,以点E为圆心的圆与直线必有两个交点
综上所述,共有四个点能与点A,点B组成直角三角形.
故选A.
 解:由题意知,直线y=-
解:由题意知,直线y=-| 1 |
| 2 |
当∠A为直角时,过点A作垂线与直线的交点W(-4,4),
当∠A为直角时,过点B作垂线与直线的交点S(2,1),
当∠C为直角时,过AB中点E(-1,0),作垂线与直线的交点为F(-1,2.5),则EF=2.5<3,
所以以3为半径,以点E为圆心的圆与直线必有两个交点
综上所述,共有四个点能与点A,点B组成直角三角形.
故选A.
点评:本题考查的是一次函数综合题,在解答此题时要分三种情况进行讨论,不要漏解.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知∠MON=30°,∠NOP=15°,则∠MOP=( )
| A、45° | B、15° |
| C、45°或15° | D、无法确定 |
 如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )
如图,在?ABCD中,AD=4cm,AB=2cm,则?ABCD的周长是( )| A、12cm | B、10cm |
| C、8cm | D、6cm |
若y与x成正比例,z与y成反比例,则z是x的( )
| A、正比例函数 | B、反比例函数 |
| C、一次函数 | D、不能确定 |
若关于x的方程||x-3|-1|=a有三个整数解,则a的值是( )
| A、3 | B、2 | C、1 | D、0 |
 如图,△ABC中,AD平分∠BAC,且AB+BD=AC,若∠B=62°,则∠C=( )
如图,△ABC中,AD平分∠BAC,且AB+BD=AC,若∠B=62°,则∠C=( )| A、62° | B、31° |
| C、87° | D、54° |
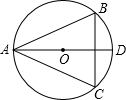 如图,AB、AC是⊙O的弦,直径AD平分∠BAC,给出下列结论:①AB=AC;②
如图,AB、AC是⊙O的弦,直径AD平分∠BAC,给出下列结论:①AB=AC;②
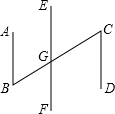 将以下各推理过程的理由填入横线内.
将以下各推理过程的理由填入横线内.