题目内容
15．先化简，再求值：$\frac{{{x^2}-2x+1}}{{{x^2}-1}}$÷（1-$\frac{3}{x+1}$），其中x=3．分析 根据分式的减法和除法可以化简题目中的式子，然后将x的值代入即可解答本题．
解答 解：$\frac{{{x^2}-2x+1}}{{{x^2}-1}}$÷（1-$\frac{3}{x+1}$）
=$\frac{（x-1）^{2}}{（x+1）（x-1）}÷\frac{x+1-3}{x+1}$
=$\frac{（x-1）^{2}}{（x+1）（x-1）}•\frac{x+1}{x-2}$
=$\frac{x-1}{x-2}$，
当x=3时，原式=$\frac{3-1}{3-2}$=2．
点评 本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
练习册系列答案
名校课堂系列答案
相关题目
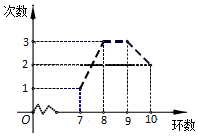一名射击运动员连续打靶9次，假如他打靶命中环数的情况如图所示，那么该射击运动员本次打靶命中环数的中位数为9环．