Question

10．已知△ABC的高AD所在直线与高BE所在直线相交于点F．
（1）如图1，若△ABC为锐角三角形，且∠ABC=45°，过点F作FG∥BC，交直线AB于点G，求证：FG+DC=AD；
（2）如图2，若∠ABC=135°，过点F作FG∥BC，交直线AB于点G，当∠DAC=60°时，判断AF、BF、BC之间的关系．

Answer 1

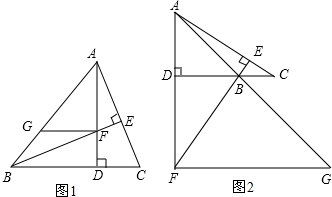
分析 （1）根据等腰直角三角形得出AD=BD，再利用全等三角形的判定和性质证明即可；
（2）结合（1）及图形我们可猜测出：FG=DC+AD；证法同（1），先证△FDB≌△CDA，得DC=DF，进而可得出FG=DC+AD的结论．

解答 （1）证明：∵∠ADB=90°，∠ABC=45°，
∴∠BAD=∠ABC=45°，
∴AD=BD；
∵∠BEC=90°，
∴∠CBE+∠C=90°，
∵∠DAC+∠C=90°，
∴∠CBE=∠DAC，
∵∠FDB=∠CDA=90°，
∴△FDB≌△CDA；
∴DF=DC；
∵GF∥BD，
∴∠AGF=∠ABC；
∴∠AGF=∠BAD；
∴FA=FG；
∴FG+DC=FA+DF=AD．
（2）解：FG=DC+AD．
∵∠ABC=135°，
∴∠ABD=45°，△ABD、△AGF皆为等腰直角三角形，
∴BD=AD，FG=AF=AD+DF；
∵∠FAE+∠DFB=∠FAE+∠DCA=90°，
∴∠DFB=∠DCA；
又∵∠FDB=∠CDA=90°，BD=AD，
在△BDF和△ADC中，
$\left\{\begin{array}{l}{∠DFB=∠DCA}\\{∠BDF=∠ADC}\\{BD=AD}\end{array}\right.$，
∴△BDF≌△ADC（AAS）；
∴DF=DC，
∴FG、DC、AD之间的数量关系为：FG=DC+AD．

点评 此题考查的是等腰直角三角形以及全等三角形的判定和性质；通过全等三角形证得CD=DF是解答此题的关键．