题目内容
15.已知关于x的方程x2+(k+2)x+k-1=0.(1)若方程的一个根为1,求k的值;
(2)若x1、x2是方程的两个实数根,且(x1-1)(x2-1)=k-3,求k的值.
分析 (1)把x=1代入原方程可得k的值;
(2)由根与系数的关系可得:x1+x2=-k-2,x1•x2=k-1,将已知等式化简后代入可得结论.
解答 解:(1)把x=1代入得:x2+(k+2)x+k-1=0.
1+k+2+k-1=0,
2k=2,
k=1,
(2)∵x1、x2是方程的两个实数根,
∴x1+x2=-k-2,x1•x2=k-1,
∴(x1-1)(x2-1)=k-3,
x1x2-x1-x2+1=k-3,
k-1-(-k-2)=k-3,
2k+1=k-3,
k=-4.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了一元二次方程的根的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列不等式变形正确的是( )
| A. | 由a>b,且c≠0,得ac<bc | B. | 若x>y,且m≠0,则-$\frac{x}{m}<-\frac{y}{m}$ | ||
| C. | 若x>y,则xz2>yz2 | D. | 若an2>bn2,则a>b |
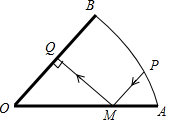 两面镜OA、OB如图放置,OA=OB=10cm,点P是$\widehat{AB}$上,PM为入射光线,且PM∥OB.
两面镜OA、OB如图放置,OA=OB=10cm,点P是$\widehat{AB}$上,PM为入射光线,且PM∥OB.
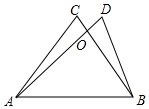 如图,△AOC≌△BOD,∠C与∠D是对应角,AC与BD是对应边,AC=8cm,AD=10cm,OD=OC=2cm,求OB的长.
如图,△AOC≌△BOD,∠C与∠D是对应角,AC与BD是对应边,AC=8cm,AD=10cm,OD=OC=2cm,求OB的长.