题目内容
8.甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.(1)若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?
(2)若丙想使球经过三次传递后,球落在自己手中的概率最大,丙会让球开始时在谁手中?请说明理由.
分析 (1)依照题意画出树状图,根据树状图即可得出经过三次传球后球传回到甲手中的概率;
(2)结合(1)的树状图,可得出从甲开始传球传球三次后传到丙手中的概率,同理,可得出从乙、丙开始传球,三次传球后传到丙手中的概率,对比后即可得出结论.
解答 解:(1)画树状图如图所示,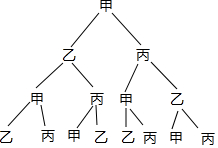
三次传球有8种等可能结果,其中传回甲手中的有2种,即甲→乙→丙→甲,甲→丙→乙→甲,
∴经过三次传球后,球传回到甲手中的概率为$\frac{2}{8}$=$\frac{1}{4}$.
(2)由树状图可知:从甲开始传球,传球三次后传到丙手中的概率为$\frac{3}{8}$,
同理:从乙开始传球,传球三次后传到丙手中的概率为$\frac{3}{8}$,从丙自己开始传球,传球三次后传到丙手中的概率为$\frac{2}{8}$=$\frac{1}{4}$,
∴丙想使球经过三次传递后,球落在自己手中的概率最大,丙会让球开始时在甲或乙手中.
点评 本题考查了列表法与树状图法,解题的关键是:(1)画出树状图;(2)观察树状图,分析从甲、乙、丙开始传球,三次传球后传到丙手中的概率.

练习册系列答案
相关题目
16.已知点A(0,2),B(4,4),点M在x轴上,当AM+BM最小时,点M的坐标为( )
| A. | (1,0) | B. | ($\frac{4}{3}$,0) | C. | ($\sqrt{2}$,0) | D. | (2,0) |
20.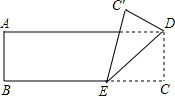 如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )
如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )
 如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )
如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
 如图,在等腰三角形ABC中,∠ACB=90°,O是AC中点,D在OB上,且OA=OD,AD的延长线交BC于E,连接CD.
如图,在等腰三角形ABC中,∠ACB=90°,O是AC中点,D在OB上,且OA=OD,AD的延长线交BC于E,连接CD. 已知△ABC与△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=BC=4,AD=DE,点F是BE的中点,连接DF,CF.
已知△ABC与△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=BC=4,AD=DE,点F是BE的中点,连接DF,CF.