题目内容
3.根据不等式的性质,把下列不等式化为x>a或x<a的形式,(1)-2x<-1;
(2)2x<-1;
(3)-2x<4x+4;
(4)$\frac{1}{2}x≥\frac{1}{3}(x-2)$.
分析 根据不等式的性质,可得答案.
解答 解:(1)-2x<-1,两边都除以-2,得
x>$\frac{1}{2}$;
(2)2x<-1,两边都除以2,得
x<-$\frac{1}{2}$;
(3)-2x<4x+4两边都减4x,得
-6x<4.
两边都除以-6,得
x>-$\frac{2}{3}$;
(4)$\frac{1}{2}x≥\frac{1}{3}(x-2)$,
两边都乘以6,得
3x≥2x-4,
两边都减2x,得
x≥-4.
点评 本题考查了不等式的性质,利用不等式的性质是解题关键.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
14.若x<-2是关于x的一元一次不等式ax-2>0的解集,则关于y的方程ay+2=0的解为( )
| A. | y=1 | B. | y=-1 | C. | y=2 | D. | y=-2 |
11.线段CD是由线段AB平移得到的,点A(4,7)的对应点为C(-1,4),则点B(-4,-1)的对应点D的坐标为( )
| A. | (-9,-4) | B. | (-1,-2) | C. | (2,9) | D. | (5,3) |
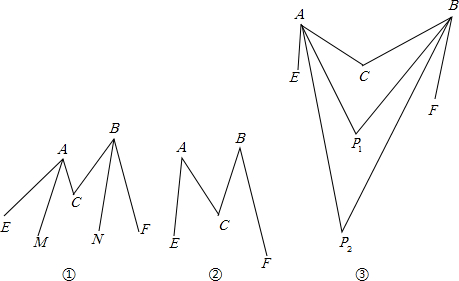
 如图,灯塔A在港口P的南偏东45°方向,距离港口20$\sqrt{2}$海里处,一艘客轮从港口P出发,沿北偏东30°方向,以20海里/小时的速度驶离港口,客轮出发后几小时后在灯塔的正北方向,并求出此时客轮距灯塔的距离.
如图,灯塔A在港口P的南偏东45°方向,距离港口20$\sqrt{2}$海里处,一艘客轮从港口P出发,沿北偏东30°方向,以20海里/小时的速度驶离港口,客轮出发后几小时后在灯塔的正北方向,并求出此时客轮距灯塔的距离.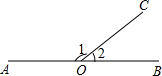 如图,点O在直线AB上,OC为射线,∠1比∠2的3倍少10°,设∠1、∠2的度数分别为x、y,则可列方程组为$\left\{\begin{array}{l}{x+y=180°}\\{x=3y-10°}\end{array}\right.$.
如图,点O在直线AB上,OC为射线,∠1比∠2的3倍少10°,设∠1、∠2的度数分别为x、y,则可列方程组为$\left\{\begin{array}{l}{x+y=180°}\\{x=3y-10°}\end{array}\right.$.