题目内容
下列式子中,正确的是( )
A. ﹣6<﹣8 B. ﹣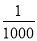 >0 C. ﹣
>0 C. ﹣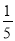 <﹣
<﹣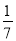 D.
D. 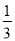 <0.3
<0.3
﹣2007的绝对值是( )
A. ﹣2007 B. ﹣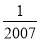 C.
C. 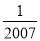 D. 2007
D. 2007
若规定收入为“+”,那么﹣50元表示( )
A.收入了50元
B.支出了50元
C.没有收入也没有支出
D.收入了100元
查看答案(1)阅读理【解析】
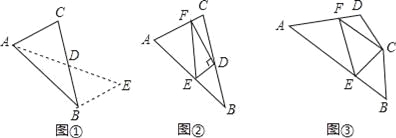
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
下面是某同学对多项式(x2﹣4x﹣3)(x2﹣4x+1)+4进行因式分解的过程.
【解析】
设x2﹣4x=y
原式=(y﹣3)(y+1)+4(第一步)
=y2﹣2y+1 (第二步)
=(y﹣1)2 (第三步)
=(x2﹣4x﹣1)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的 .
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)请你模仿以上方法尝试对多项式(x2+2x)(x2+2x+2)+1进行因式分解.
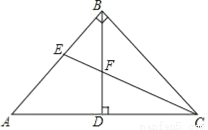
查看答案如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.
(1)求证:△BEF是等腰三角形;
(2)求证:BD=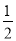 (BC+BF).
(BC+BF).
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 阅读快车系列答案
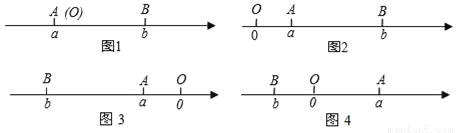
阅读快车系列答案阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
(1)3;3;7;(2)|x+1|,1或﹣3;(3)4. 【解析】试题分析:(1)数轴上表示2和5的两点之间的距离是|5-2|=3,-2和-5的两点之间的距离是|-2-(-5)|=3,表示-2和5的两点之间的距离是|5-(-2)|=7;(2)数轴上表示x和-1的两点A和B之间的距离是|x-(-1)|=|x+1|,令|x+1|=2,解得x=1或-3;(3)代数式|x-1|+|x+3|表示数轴上...甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.某顾客购买的电器价格是x元.
(1)当x=850时,该顾客应选择在 商场购买比较合算;
(2)当x>1000时,分别用代数式表示在两家商场购买电器所需付的费用;
(3)当x=1700时,该顾客应选择哪一家商场购买比较合算?说明理由.
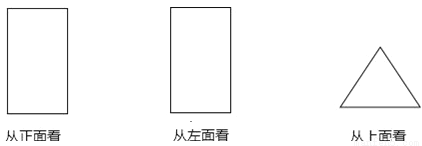
查看答案已知如图为一几何体的三种形状图:
(1)这个几何体的名称为 ;
(2)任意画出它的一种表面展开图;
(3)若从正面看到的是长方形,其长为10cm;从上面看到的是等边三角形,其边长为4cm,求这个几何体的侧面积.
司机小王沿东西大街跑出租车,约定向东为正,向西为负,某天自A地出发到收工时,行走记录为(单位:千米):+8、﹣9、+7、﹣2、+5、﹣10、+7、﹣3,回答下列问题
(1)收工时小王在A地的哪边?距A地多少千米?
(2)若每千米耗油0.2升,问从A地出发到收工时,共耗油多少升?
(3)在工作过程中,小王最远离A地多远?
查看答案化简与求值:
(1)化简: 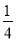 (﹣4x2+2x﹣8)﹣(
(﹣4x2+2x﹣8)﹣(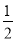 x﹣1)
x﹣1)
(2)先化简,再求值:2(a2b+ab2)﹣2(a2b﹣1)﹣2ab2﹣2,其中a=﹣2,b=2.
查看答案计算:
(1)16÷(﹣23)﹣(﹣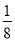 )×(﹣4)
)×(﹣4)
(2)﹣4﹣(﹣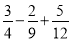 )÷
)÷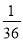
(3)﹣14﹣[2﹣(﹣3)2]÷(﹣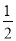 )3.
)3.
- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若圆锥的底面半径为3,母线长为6,则圆锥的侧面积等于_____.
18π 【解析】试题分析:根据圆锥的侧面积就等于经母线长乘底面周长的一半.依此公式计算即可解决问题. 圆锥的侧面积=6×6π÷2=18π. 故答案为:18π.已知四边形ABCD内有一点E,满足EA=EB=EC=ED,且∠BCD=130°,那么∠BAD的度数为_____.
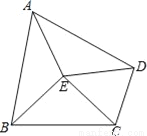
某校男子足球队队员的年龄分布为如图的条形图,则这些队员年龄的众数、中位数分别是_____。
现有60件某种产品,其中有3件次品,那么从中任意抽取1件产品恰好抽到次品的概率是_____。
查看答案如图,水平地面上有一面积为30πcm2的灰色扇形OAB,其中OA=6cm,且OA垂直于地面,将这个扇形向右滚动(无滑动)至点B刚好接触地面为止,则在这个滚动过程中,点O移动的距离是( )
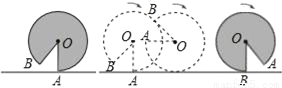
A. 10πcm B. 20πcm C. 24πcm D. 30πcm
查看答案若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是( )
A. k>﹣1 B. k>﹣1且k≠0 C. k<1 D. k<1且k≠0
查看答案 试题属性- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
数轴上到点﹣3的距离是3个单位长度的点表示的数是_____.
0或﹣6. 【解析】试题分析:在数轴上两点所表示的数的差的绝对值为这两个点之间的距离.设这个点表示的数为x,则,则,解得:x=0或-6,即这个点表示的数为0或-6.已知单项式3amb2与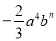 的和是单项式,那么m=_____,n=_____.
的和是单项式,那么m=_____,n=_____.
某种零件,标明要求是φ20±0.02 mm(φ表示直径,单位:毫米),经检查,一个零件的直径是19.9 mm,该零件________ (填“合格”或“不合格”).
查看答案我国2006年参加高考报名的总人数约为950万人,则该人数可用科学记数法表示为_____人.
查看答案若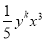 与
与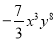 是同类项,则k=_____.
是同类项,则k=_____.
单项式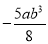 的系数是 ,次数是 .
的系数是 ,次数是 .
- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某种品牌的彩电降价30%以后,每台售价为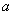 元,则该品牌彩电每台原价应为( )
元,则该品牌彩电每台原价应为( )
A. 0.7a元 B. 0.3a元 C. 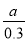 元 D.
元 D. 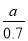 元
元
用四舍五入法按要求对0.05019分别取近似值,其中错误的是( )
A. 0.1(精确到0.1) B. 0.05(精确到千分位)
C. 0.05(精确到百分位) D. 0.0502(精确到0.0001)
查看答案下列各式计算中,正确的是( )
A. 2a+2=4a B. ﹣2x2+4x2=2x2 C. x+x=x2 D. 2a+3b=5ab
查看答案下列说法正确的是( )
A. 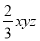 与
与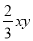 是同类项 B.
是同类项 B. 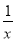 和
和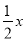 是同类项
是同类项
C. 0.5x3y2与7x2y3是同类项 D. 5m2n与﹣4nm2是同类项
查看答案下列各式中,等号不成立的是( )
A. |﹣4|=4 B. ﹣|4|=|﹣4| C. |﹣4|=|4| D. ﹣|﹣4|=﹣4
查看答案下列式子中,正确的是( )
A. ﹣6<﹣8 B. ﹣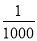 >0 C. ﹣
>0 C. ﹣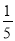 <﹣
<﹣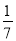 D.
D. 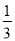 <0.3
<0.3
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.
(1)求证:△BEF是等腰三角形;
(2)求证:BD=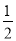 (BC+BF).
(BC+BF).

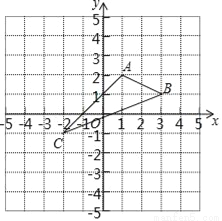
在平面直角坐标系中,A(1,2)、B(3,1)、C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出△ABC关于x轴对称△A2B2C2的各项点坐标A2 ,B2 ,C2 ;
(3)求△ABC的面积.
(1)已知x+y=15,x2+y2=113,求x2﹣3xy+y2的值;
(2)先化简,再求值:(2x﹣1)2﹣(3x+1)(3x﹣1)+5x(x﹣1),x=﹣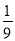 .
.
(1)(﹣2a2)3+2a2•a4;
(2)(x+y)2﹣(x+y)(x﹣y)
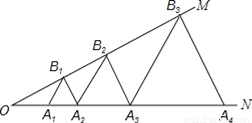
查看答案如图,已知∠MON=30°,点A1、A2、A3,…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4 …均为等边三角形,若OA1=1,则△A2016B2016A2017的边长为_____.
已知a2﹣a﹣1=0,则a2﹣a+2017=_____.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在平面直角坐标系xOy中,已知点A(2,﹣2),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的有( )个.
A. 5 B. 4 C. 3 D. 2
B 【解析】试题解析:∵A(2,?2), ①如图:若OA=AP,则 ②如图:若OA=OP,则 ③如图:若OP=AP,则 综上可得:符合条件的点P有四解. 故选B.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式.下列三个代数式:①(a﹣b)2;②ab+bc+ca;③a2b+b2c+c2a.其中是完全对称式的是( )
A. ①②③ B. ①③ C. ②③ D. ①②
查看答案如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下三个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°.
其中结论正确的个数是( )
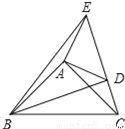
A. 1 B. 2 C. 3 D. 0
查看答案已知10m=2,10n=3,则103m+2n=( )
A. 17 B. 72 C. 12 D. 36
查看答案在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图(1),然后拼成一个梯形,如图(2),根据这两个图形的面积关系,表明下列式子成立的是( )
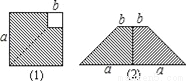
A. a2﹣b2=(a+b)(a﹣b) B. (a+b)2=a2+2ab+b2
C. (a﹣b)2=a2﹣2ab+b2 D. a2﹣b2=(a﹣b)2
查看答案下列因式分解不正确的是( )
A. x2﹣6x+9=(x﹣3)2 B. x2﹣y2=(x﹣y)2
C. x2﹣5x+6=(x﹣2)(x﹣3) D. 6x2+2x=2x(3x+1)
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在数轴上有三个点A,B,C,分别表示﹣3,0,2.按下列要求回答:
(1)点A向右移动6个单位后,三个点表示的数谁最大?
(2)点C向左移动3个单位后,这时点B表示的数比点C表示的数大多少?
(3)怎样移动点A,B,C中的两个点,才能使三个点所表示的数相同?有几种办法?分别写出来.
(1)A;(2)1;(3)3种,具体见解析. 【解析】试题分析:画出数轴,标出A、B、C三点,然后根据变化规律求解,(1)中注意A点的移动后的坐标;(2)中先求出C移动后的数为-1,然后比较即可;(3)分情况变化比较即可. 试题解析:(1)点A表示的数最大,是+3. (2)C移动后是-2,B点比C点大1.[0-(-1)=1] (3)有三种方法:①种:将A向右移动3个单位,C向左移动...计算
(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣9);
(2)﹣0.5﹣(﹣3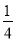 )+2.75﹣7
)+2.75﹣7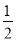 ;
;
(3)(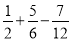 )×(﹣36);
)×(﹣36);
(4)﹣14﹣(5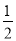 )×
)×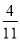 +(﹣2)3+|32+1|
+(﹣2)3+|32+1|
把下列各数填入相应的大括号内:
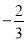 ,
, 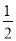 ,﹣0.01,
,﹣0.01, 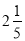 ,7,1,﹣(﹣4),+(﹣1)
,7,1,﹣(﹣4),+(﹣1)
正数集合{ …}
负数集合{ …}
非负整数集合{ …}
分数集合{ …}.
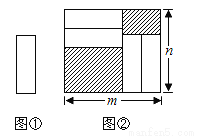
查看答案把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长和是_____cm.(用m或n的式子表示).
单项式﹣2xy5的系数是m,次数是n,则m﹣n=_____.
查看答案一列单项式﹣x2,3x3,﹣5x4,7x5.…,按此规律排列,则第9个单项式是_____.
查看答案 试题属性- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
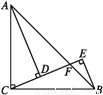
如图,在△ABC中,∠ACB=90°,AC=BC,CE⊥BE于点E,CE与AB交于点F,AD⊥CF于点D,且AD平分∠FAC.请写出图中两对全等三角形,并选择其中一对加以说明.
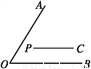
如图,已知∠AOB=α,且PC∥OB,现以P为顶点,PC为一边作∠CPD=α,并用移动三角尺的方法验证,PD与OA是否平行.
某商场为了吸引更多的顾客,安排了一个抽奖活动,并规定:顾客每购买100元商品,就能获得一次抽奖的机会.抽奖规则如下:在抽奖箱内,有100个牌子,分别写有1,2,3,…,100共100个数字,抽到末位数是5的可获20元购物券,抽到数字是88的可获200元购物券,抽到66或99的可获100元购物券.某顾客购物用了130元,他获得购物券的概率是多少?他获得20元、100元、200元购物券的概率分别是多少?
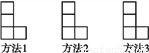
查看答案在由小正方形组成的L形的图形中,用三种不同的方法添画一个小正方形,使它成为轴对称图形.
如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律摆.
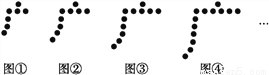
(1)第5个“广”字中的棋子个数是 .
(2)第n个“广”字需要多少枚棋子?
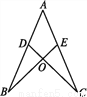
查看答案如图,点D在AB上,点E在AC上,AB=AC,AD=AE.试说明∠B=∠C.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

