题目内容
在数轴上有三个点A,B,C,分别表示﹣3,0,2.按下列要求回答:
(1)点A向右移动6个单位后,三个点表示的数谁最大?
(2)点C向左移动3个单位后,这时点B表示的数比点C表示的数大多少?
(3)怎样移动点A,B,C中的两个点,才能使三个点所表示的数相同?有几种办法?分别写出来.
(1)A;(2)1;(3)3种,具体见解析. 【解析】试题分析:画出数轴,标出A、B、C三点,然后根据变化规律求解,(1)中注意A点的移动后的坐标;(2)中先求出C移动后的数为-1,然后比较即可;(3)分情况变化比较即可. 试题解析:(1)点A表示的数最大,是+3. (2)C移动后是-2,B点比C点大1.[0-(-1)=1] (3)有三种方法:①种:将A向右移动3个单位,C向左移动...计算
(1)(﹣3)+(﹣4)﹣(+11)﹣(﹣9);
(2)﹣0.5﹣(﹣3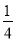 )+2.75﹣7
)+2.75﹣7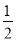 ;
;
(3)(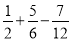 )×(﹣36);
)×(﹣36);
(4)﹣14﹣(5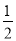 )×
)×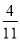 +(﹣2)3+|32+1|
+(﹣2)3+|32+1|
把下列各数填入相应的大括号内:
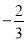 ,
, 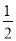 ,﹣0.01,
,﹣0.01, 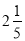 ,7,1,﹣(﹣4),+(﹣1)
,7,1,﹣(﹣4),+(﹣1)
正数集合{ …}
负数集合{ …}
非负整数集合{ …}
分数集合{ …}.
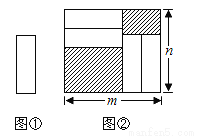
查看答案把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长和是_____cm.(用m或n的式子表示).
单项式﹣2xy5的系数是m,次数是n,则m﹣n=_____.
查看答案一列单项式﹣x2,3x3,﹣5x4,7x5.…,按此规律排列,则第9个单项式是_____.
查看答案 试题属性- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案某旅行社的一则广告如下:我社推出去井冈山红色旅游,收费标准为:如果组团人数不超过30人,人均收费800元;如果人数多于30人,那么每增加1人,人均收费降低10元,但人均收费不得低于500元,甲公司想分批组织员工到井冈山红色旅游学习.
(1)如果第一批组织38人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
(1)27360;(2)应安排45人参加 【解析】试题分析: (1)由题意可列出式子:38×[800﹣(38﹣30)×10]计算可得结果; (2)首先由30×800=24000<29250,可知这次去旅游的人数超过了30人, 设安排了人去旅游,由题意可列方程: ,解方程求得的值后,再由人均费用不低于500元进行检验即可得到答案. 试题解析: (1)∵人数多于30...甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之和能被3整除的概率.
查看答案已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求k的值.
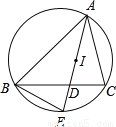
查看答案如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.求证:IE=BE.
市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,分别计算甲、乙的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
查看答案解方程:(1)2x2﹣5x+2=0;
(2)x+3﹣x(x+3)=0.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列式子中,正确的是( )
A. ﹣6<﹣8 B. ﹣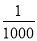 >0 C. ﹣
>0 C. ﹣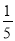 <﹣
<﹣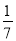 D.
D. 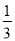 <0.3
<0.3
﹣2007的绝对值是( )
A. ﹣2007 B. ﹣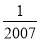 C.
C. 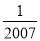 D. 2007
D. 2007
若规定收入为“+”,那么﹣50元表示( )
A.收入了50元
B.支出了50元
C.没有收入也没有支出
D.收入了100元
查看答案(1)阅读理【解析】
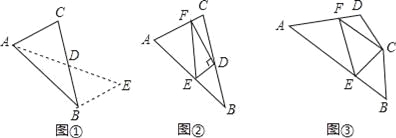
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
下面是某同学对多项式(x2﹣4x﹣3)(x2﹣4x+1)+4进行因式分解的过程.
【解析】
设x2﹣4x=y
原式=(y﹣3)(y+1)+4(第一步)
=y2﹣2y+1 (第二步)
=(y﹣1)2 (第三步)
=(x2﹣4x﹣1)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的 .
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)请你模仿以上方法尝试对多项式(x2+2x)(x2+2x+2)+1进行因式分解.
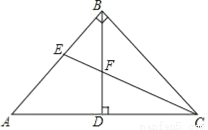
查看答案如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D;CE平分∠ACB,交AB于点E,交BD于点F.
(1)求证:△BEF是等腰三角形;
(2)求证:BD=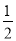 (BC+BF).
(BC+BF).
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列因式分解不正确的是( )
A. x2﹣6x+9=(x﹣3)2 B. x2﹣y2=(x﹣y)2
C. x2﹣5x+6=(x﹣2)(x﹣3) D. 6x2+2x=2x(3x+1)
B 【解析】试题解析:A. 正确; B. 故错误; C. 正确; D. 正确; 故选B.长方形的面积为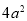 ﹣6ab+2a,若它的一边长为2a,则它的周长为( ).
﹣6ab+2a,若它的一边长为2a,则它的周长为( ).
A.4a﹣3b B.8a﹣6b C.4a﹣3b+1 D.8a﹣6b+2
查看答案如果x2+( )x+25是完全平方式,横线处填( )
A. 5 B. 10 C. ±5 D. ±10
查看答案如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
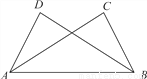
A. AC=BD B. ∠CAB=∠DBA
C. ∠C=∠D D. BC=AD
查看答案下列计算正确的是( )
A.a2+a3=a5 B.a2•a3=a6
C.(a2)3=a5 D.a5÷a2=a3
查看答案如图,在Rt△ABC中,∠BAC=90°,AB=AC,点A,点C分别在直线a,b上,且a∥b.若∠1=60°,则∠2的度数为( )
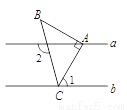
A. 75° B. 105° C. 135° D. 155°
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知多项式A,B,计算A﹣B.某同学做此题时误将A﹣B看成了A+B,求得其结果为A+B=3m2﹣2m﹣5,若B=2m2﹣3m﹣2,请你帮助他求得正确答案.
. 【解析】试题分析:根据整式的加减的互逆性,求出A,然后再求A-B即可. 试题解析:∵A+B=3m2﹣2m﹣5,B=2m2﹣3m﹣2 ∴A=(3m2﹣2m﹣5)-(2m2﹣3m﹣2) =3 m2-2m-5-2 m2+3m+2 = m2+m-3 ∴A-B=(m2+m-3)-(2m2﹣3m﹣2) =m2+m-3-2m2+3m+2 =- m2+4m-1 ...已知|a﹣2|+(b+1)2=0,求5ab2﹣|2a2b﹣(4ab2﹣2a2b)|的值.
查看答案出租车司机老李某天上午营运全是在东西走向的胜利路上进行,如果规定向东为正,向西为负,他这天上午行车里程(单位:公里 )如下:
+8,+4,﹣10,﹣8,+6,﹣2,﹣5,﹣7,+4,+6,﹣8,﹣9
(1)将第几名乘客送到目的地时,老王刚好回到上午出发点?
(2)将最后一名乘客送 到目的地时,老王距上午出发点多远?
(3)若汽车耗油量为0.4升/公里,这天上午老王耗油多少升?
查看答案先化简,再求值.
(1)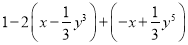 ,其中x=﹣
,其中x=﹣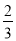 ,y=﹣1.
,y=﹣1.
(2)﹣a2b+(3ab2﹣a2b)﹣2(2ab2﹣a2b),其中a=1,b=﹣2.
查看答案若有理数m、n在数轴上的位置如图所示,请化简:|m+n|+|m﹣n|﹣|n|.
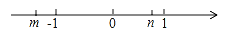
在数轴上有三个点A,B,C,分别表示﹣3,0,2.按下列要求回答:
(1)点A向右移动6个单位后,三个点表示的数谁最大?
(2)点C向左移动3个单位后,这时点B表示的数比点C表示的数大多少?
(3)怎样移动点A,B,C中的两个点,才能使三个点所表示的数相同?有几种办法?分别写出来.
查看答案 试题属性- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一列单项式﹣x2,3x3,﹣5x4,7x5.…,按此规律排列,则第9个单项式是_____.
. 【解析】根据式子的特点,可知各项符号为:(-1)2n-1,系数为2n-1,而x的指数为n+1,因此可知其规律为:(-1)2n-1xn+1,则第9个为:(-1)2n-1(2n-1)xn+1=(-1)2×9-1(2×9-1)x9+1=-17x10. 故答案为: .在3,﹣4,6,﹣7这四个数中,任取两个数相乘,所得的积最大的是_____.
查看答案若a、b互为倒数,则(﹣ab)2017=_____.
查看答案x2+ax﹣y﹣(bx2﹣x+9y+3)的值与x的取值无关,则﹣a+b的值为( )
A. 0 B. ﹣1 C. ﹣2 D. 2
查看答案一个多项式与x2﹣3x+2的和是3x﹣1,则这个多项式为( )
A. ﹣x2+6x+1 B. ﹣x2+1 C. ﹣x2+6x﹣3 D. ﹣x2﹣6x+1
查看答案下列运算正确的是( )
A. ﹣a2b﹣2a2b=﹣3a2b B. 2a﹣a=2a
C. 3a2+2a2=5a4 D. 2a+b=2ab
查看答案 试题属性- 题型:填空题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列式子:x2+2, 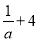 ,
, 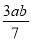 ,
, 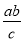 ,﹣5x,0中,整式的个数有( )
,﹣5x,0中,整式的个数有( )
A. 3个 B. 4个 C. 5个 D. 6个
B 【解析】根据整式是有理式的一部分,在有理式中可以包含加,减,乘,除四种运算,但在整式中除数不能含有字母。单项式和多项式都统称为整式。因此可知x2+2, ,﹣5x,0是整式,故有4个. 故选:B.我国作家莫言获得诺贝尔文学奖之后,他的代表作品《蛙》的销售量就比获奖之前增长了180倍,达到2100000册,将2100000用科学记数法表示为( )
A. 0.21×108 B. 2.1×106 C. 2.1×107 D. 21×106
查看答案两个数的和为正数,那么这两个数是( )
A. 正数 B. 负数
C. 至少有一个为正数 D. 一正一负
查看答案若|x|=4,|y|=7,且x+y>0,那么x﹣y的值是( )
A. 3或11 B. 3或﹣11 C. ﹣3或11 D. ﹣3或﹣11
查看答案数轴上一点A,一只蚂蚁从A出发爬了4个单位长度到了原点,则点A所表示的数是( )
A. 4 B. ﹣4 C. ±8 D. ±4
查看答案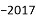
A. 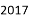
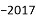
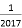 D.
D. 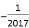
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在3,﹣4,6,﹣7这四个数中,任取两个数相乘,所得的积最大的是_____.
28. 【解析】根据有理数的乘法,同号得正,异号的负,并把绝对值相乘,分别取四个数中的两个计算,比较可求解:3×(-4)=-12,3×6=18,3×(-7)=-21,(-4)×6=-24,(-4)×(-7)=28,6×(-7)=-42,最大的乘积为28. 故答案为:28.若a、b互为倒数,则(﹣ab)2017=_____.
查看答案x2+ax﹣y﹣(bx2﹣x+9y+3)的值与x的取值无关,则﹣a+b的值为( )
A. 0 B. ﹣1 C. ﹣2 D. 2
查看答案一个多项式与x2﹣3x+2的和是3x﹣1,则这个多项式为( )
A. ﹣x2+6x+1 B. ﹣x2+1 C. ﹣x2+6x﹣3 D. ﹣x2﹣6x+1
查看答案下列运算正确的是( )
A. ﹣a2b﹣2a2b=﹣3a2b B. 2a﹣a=2a
C. 3a2+2a2=5a4 D. 2a+b=2ab
查看答案多项式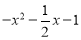 的各项分别是 ( )
的各项分别是 ( )
A、 B、
B、 C、
C、 D、
D、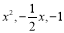
- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
(本小题满分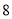 分)
分)
如图, 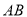 是⊙
是⊙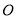 的直径,点
的直径,点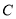 是⊙
是⊙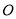 上一点,连接
上一点,连接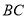 ,
, 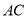 ,
, 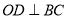 于
于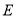 .
.
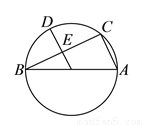
(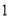 )求证:
)求证: 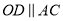 .
.
(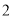 )若
)若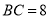 ,
, 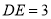 ,求⊙
,求⊙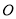 的直径.
的直径.
二次函数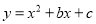 的图象经过点
的图象经过点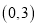 ,
, 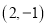 .
.
(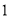 )求
)求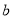 ,
, 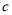 的值;
的值;
(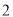 )求该二次函数图象的对称轴及与
)求该二次函数图象的对称轴及与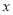 轴交点坐标.
轴交点坐标.
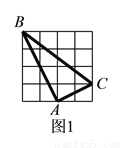
如图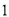 ,在
,在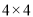 的正方形方格中,
的正方形方格中, 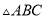 的顶点都在边长为
的顶点都在边长为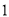 的小正方形的顶点.
的小正方形的顶点.
(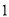 )填空:
)填空: 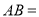 __________,
__________, 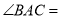 __________
__________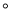 ;
;
( )请在图
)请在图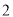 中的两个
中的两个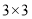 的正方形方格中各画一个和
的正方形方格中各画一个和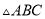 相似但不全等的格点三角形.
相似但不全等的格点三角形.

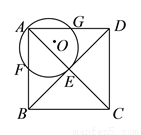
如图,在正方形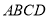 中,
中, 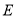 为对角线
为对角线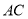 ,
, 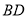 的交点,经过点
的交点,经过点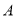 和点
和点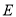 作⊙
作⊙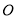 ,分别交
,分别交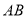 ,
, 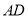 于点
于点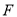 ,
, 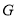 .已知正方形边长为
.已知正方形边长为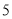 ,⊙
,⊙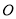 的半径为
的半径为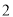 ,则
,则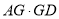 的值为__________.
的值为__________.
如图,抛物线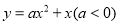 交
交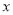 轴于点
轴于点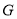 ,
, 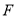 ,交
,交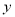 轴于点
轴于点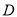 ,在
,在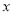 轴上方的抛物线上有两点
轴上方的抛物线上有两点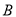 ,
, 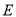 ,它们关于
,它们关于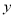 轴对称,点
轴对称,点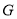 ,
, 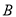 在
在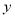 轴左侧,
轴左侧, 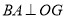 于点
于点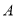 ,
, 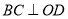 于点
于点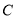 ,四边形
,四边形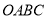 与四边形
与四边形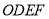 的面积分别为
的面积分别为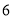 和
和 ,则
,则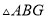 与
与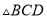 的面积之和为__________.
的面积之和为__________.
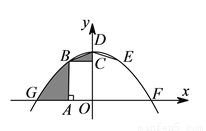
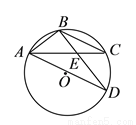
如图,已知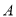 ,
, 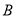 ,
, 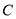 ,
, 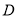 是⊙
是⊙ 上的四个点,
上的四个点, 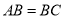 ,
, 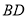 交
交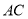 于点
于点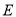 ,连接
,连接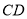 ,
, 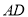 .若
.若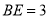 ,
, 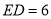 ,则
,则 __________.
__________.
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

