题目内容
在平面直角坐标系xOy中,已知两点A(0,3),B(1,0),现将线段AB绕点B按顺时针方向旋转90°得到线段BC,抛物线y=ax2+bx+c(a≠0)经过点C.
(1)如图1,若该抛物线经过原点O,且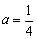 .
.
①求点C的坐标及该抛物线的表达式;
②在抛物线上是否存在点P,使得∠POB=∠BAO. 若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点D(2,1),点Q在抛物线上,且满足∠QOB=∠BAO. 若符合条件的Q点的个数是4个,请直接写出a的取值范围.

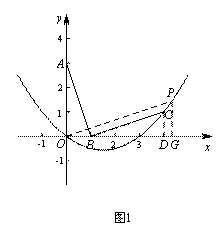
解:(1)①如图1,过点C作CD⊥x轴于点D.
∴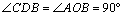 .
.
 ∵∠ABC=90º,
∵∠ABC=90º,
∴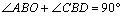 .
.
又∵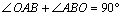 ,
,
∴ .
.
∵AB=BC,
∴△AOB≌△BDC.
∴BD=OA,CD=OB.
∵A(0,3),B(1,0),
∴C(4,1).
∵抛物线y=ax2+bx+c经过原点O,且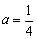 ,
,
∴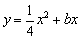 .
.
又∵抛物线经过点C(4,1),
∴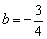 .
.
∴该抛物线的表达式为 .
.
② 当点P在第一象限时,过点P作PG⊥x轴于点G,连接OP.
∵∠POB=∠BAO,
∴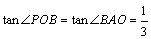 .
.
设P(3m,m),m>0.
∵点P在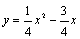 上,
上,
∴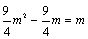 .
.
解得: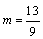 ,
,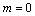 (舍去).
(舍去).
∴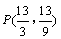 .
.
当点P在第四象限时,同理可求得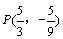 .
.
当点P在第二、三象限时,∠POB为钝角,不符合题意.
综上所述,在抛物线上存在使得∠POB=∠BAO的点P,点P的坐标为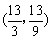 或
或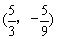 .
.
(2)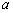 的取值范围为
的取值范围为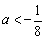 或
或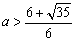 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,三角形PCQ的面积为
,三角形PCQ的面积为 ,三角形PAQ的面积为
,三角形PAQ的面积为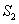 ,三角形ABP的面积为
,三角形ABP的面积为 .
.  (用含t的代数式表示);
(用含t的代数式表示);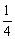
 值,若不存在,说明理由.
值,若不存在,说明理由.
 .
.


 中任取一个点,则该点在
中任取一个点,则该点在 的图像上的概率是_________.
的图像上的概率是_________.