题目内容
6.计算:(1)$\sqrt{8}$+3$\sqrt{\frac{1}{3}}$-$\frac{1}{\sqrt{2}}$+$\frac{\sqrt{3}}{2}$.
(2)5$\sqrt{2}$+$\sqrt{8}$-7$\sqrt{18}$
(3)($\sqrt{2}$+$\sqrt{3}$)2(5-2$\sqrt{6}$).
分析 (1)化简二次根式,然后合并二次根式;
(2)化简二次根式,然后合并二次根式;
(3)根据乘法公式进行计算.
解答 解:(1)$\sqrt{8}$+3$\sqrt{\frac{1}{3}}$-$\frac{1}{\sqrt{2}}$+$\frac{\sqrt{3}}{2}$
=2$\sqrt{2}$+$\sqrt{3}$-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$
=$\frac{3}{2}$$\sqrt{2}$+$\frac{3}{2}$$\sqrt{3}$;
(2)5$\sqrt{2}$+$\sqrt{8}$-7$\sqrt{18}$
=5$\sqrt{2}$+2$\sqrt{2}$-21$\sqrt{2}$
=-14$\sqrt{2}$;
(3)($\sqrt{2}$+$\sqrt{3}$)2(5-2$\sqrt{6}$)
=(5+2$\sqrt{6}$)(5-2$\sqrt{6}$)
=25-24
=1.
点评 本题考查了二次根式的混合运算,熟练掌握运算法则是解题的关键.

练习册系列答案
相关题目
1.△ABC的三边长分别是1、k、3,则化简$7-\sqrt{4{k^2}-36k+81}-|{2k-3}|$的结果为( )
| A. | -5 | B. | 19-4k | C. | 13 | D. | 1 |
11.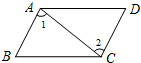 如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是( )
如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是( )
 如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是( )
如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是( )| A. | AB∥CD | B. | AD∥BC | C. | ∠B=∠D | D. | ∠DCA=∠DAC |
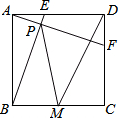 如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为2$\sqrt{10}$.
如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为2$\sqrt{10}$.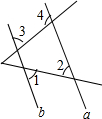 如图,∠1=60°,∠2=60°,∠3=80°,求∠4的度数.
如图,∠1=60°,∠2=60°,∠3=80°,求∠4的度数.
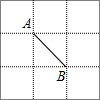 如图,在3×3的网格中,每个网格线的交点称为格点.已知图中A,B两个格点,请在图中再寻找另一个格点C,使△ABC成为等腰三角形,则满足条件的点C有8个.
如图,在3×3的网格中,每个网格线的交点称为格点.已知图中A,B两个格点,请在图中再寻找另一个格点C,使△ABC成为等腰三角形,则满足条件的点C有8个.