题目内容
14.下列各组数据中能作为直角三角形的三边长的是( )| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 1,1,$\sqrt{3}$ | C. | 4,5,6 | D. | 1,$\sqrt{3}$,2 |
分析 根据勾股定理的逆定理对各选项进行逐一分析即可.
解答 解:A、∵($\sqrt{3}$)2+($\sqrt{4}$)2≠($\sqrt{5}$)2,∴此组数据不能作为直角三角形的三边长,故本选项错误;
B、∵12+12=2≠($\sqrt{3}$)2,∴此组数据不能作为直角三角形的三边长,故本选项错误;
C、∵42+52=41≠62,∴此组数据不能作为直角三角形的三边长,故本选项错误;
D、∵12+($\sqrt{3}$)2=4=22,∴此组数据能作为直角三角形的三边长,故本选项正确.
故选D.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
4.对有理数x,y定义新运算:x?y=ax+by+1,其中a,b是常数.若2?(-1)=-3,3?3=4,则a,b的值分别为( )
| A. | a=1,b=2 | B. | a=-1,b=2 | C. | a=-1,b=-2 | D. | a=1,b=-2 |
5.某市2017年有25000名学生参加中考,为了了解这25000名考生的中考成绩,从中抽取了1000名考生的成绩进行分析,以下说法正确的是( )
| A. | 25000名考生是总体 | B. | 每名考生的成绩是个体 | ||
| C. | 1000名考生是总体的一个样本 | D. | 样本容量是25000 |
2.△ABC中,∠C=80°,∠A-∠B=20°,则∠A的度数是( )
| A. | 60° | B. | 40° | C. | 30° | D. | 20° |
19.下列不等式的变形正确的是( )
| A. | 若am>bm,则a>b | B. | 若am2>bm2,则a>b | ||
| C. | 若a>b,则am2>bm2 | D. | 若a>b且ab>0,则$\frac{1}{a}$>$\frac{1}{b}$ |
6.下列计算正确的是( )
| A. | (ab)2=a2b2 | B. | 2(a+1)=2a+1 | C. | a2+a3=a6 | D. | a6÷a2=a3 |
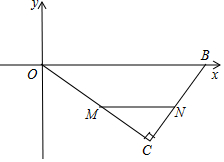 已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.
已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N.