题目内容
6.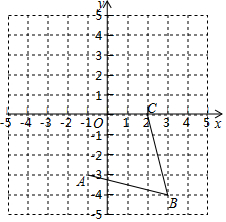 在正方形网格中,我们把每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.
在正方形网格中,我们把每个小正方形的顶点叫做格点,连接任意两个格点的线段叫网格线段,以网格线段为边组成的图形叫做格点图形,如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.(1)请在所给的网格内画出以线段AB,BC为边的菱形,并写出点D的坐标(-2,1);
(2)求线段BC的长,菱形ABCD的面积.
分析 (1)在网格中找出D,连接得到菱形ABCD,进而得出D坐标即可;
(2)利用勾股定理求出BC,AC,BD的长,根据菱形面积等于两对角线乘积的一半,求出即可.
解答  解:(1)如图所示,菱形ABCD为所求,此时D坐标为(-2,1);
解:(1)如图所示,菱形ABCD为所求,此时D坐标为(-2,1);
故答案为:(-2,1);
(2)根据勾股定理得:BC=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$;AC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$;BD=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$,
则S菱形ABCD=$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×3$\sqrt{2}$×5$\sqrt{2}$=15.
点评 此题考查了作图-应用与设计作图,勾股定理,以及菱形的判定与性质,作出正确的图形是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.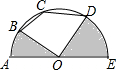 如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )
如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )
 如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )
如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )| A. | 2π | B. | 4π | C. | 8π | D. | 16π |