题目内容
 如图,马航370失联后,“海巡31”船匀速在印度洋搜救,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B,海巡船继续向北航行4小时后到达C处,发现灯塔B在它的北偏东60°方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔B最近?( )
如图,马航370失联后,“海巡31”船匀速在印度洋搜救,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B,海巡船继续向北航行4小时后到达C处,发现灯塔B在它的北偏东60°方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔B最近?( )| A、1小时 | ||
| B、2小时 | ||
C、
| ||
D、2
|
考点:解直角三角形的应用-方向角问题
专题:
分析:过B作AC的垂线,设垂足为D.由题易知:∠DAB=30°,∠DCB=60°,则∠CBD=∠CBA=30°,得AC=BC.根据BC(即AC)的长求出CD的长的关系,进而可求出该船需要继续航行的时间.
解答: 解:作BD⊥AC于D,如下图所示:
解:作BD⊥AC于D,如下图所示:
易知:∠DAB=30°,∠DCB=60°,
则∠CBD=∠CBA=30°.
∴AC=BC,
可得∠DBC=30°,
故CD=
BC,
∵海巡船从A点继续向北航行4小时后到达C处,
∴海巡船继续向北航行2小时到达D处.
故选:B.
 解:作BD⊥AC于D,如下图所示:
解:作BD⊥AC于D,如下图所示:易知:∠DAB=30°,∠DCB=60°,
则∠CBD=∠CBA=30°.
∴AC=BC,
可得∠DBC=30°,
故CD=
| 1 |
| 2 |
∵海巡船从A点继续向北航行4小时后到达C处,
∴海巡船继续向北航行2小时到达D处.
故选:B.
点评:本题考查了解直角三角形的应用中的方向角问题,注意掌握“化斜为直”是解三角形的常规思路,需作垂线(高),原则上不破坏特殊角(30°、45°60°).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式m2-m+2008的值为( )
| A、2009 | B、2008 |
| C、2007 | D、2006 |
 如图,A是正方体小木块(质地均匀)的一顶点,将其随机投掷在水平桌面上,则A点的棱长与桌面接触的概率
如图,A是正方体小木块(质地均匀)的一顶点,将其随机投掷在水平桌面上,则A点的棱长与桌面接触的概率
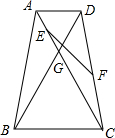 如图,梯形ABCD中,AD∥BC,AB=DC,AC交BD于G,且cos∠BGC=
如图,梯形ABCD中,AD∥BC,AB=DC,AC交BD于G,且cos∠BGC= 已知:如图,AB∥CD,∠B=∠C.求证:∠E=∠F.(本题需要标注理由)
已知:如图,AB∥CD,∠B=∠C.求证:∠E=∠F.(本题需要标注理由) 将一副三角板如图所示叠放,A、E、C、D在同一条直线上.
将一副三角板如图所示叠放,A、E、C、D在同一条直线上.