Question

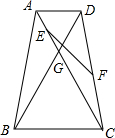如图，梯形ABCD中，AD∥BC，AB=DC，AC交BD于G，且cos∠BGC=

1

2

，E、F分别为AG、DC的中点．EF=6cm．
（1）求证：△BGC为正三角形；
（2）求等腰梯形的腰长．

Answer 1

考点：全等三角形的判定与性质,等边三角形的判定与性质,等腰梯形的性质

专题：

分析：（1）根据已知条件先求得△ABC≌DCB，得出对应角相等，然后依据三角函数求得∠BGC=60°得出结果．
（2）依据等边三角形的性质，看求得三角形DEC为直角三角形，再依据直角三角形的性质求得．

解答：（1）证明∵梯形ABCD中，AD∥BC，AB=DC
∴梯形ABCD是等腰梯形
∴∠ABC=∠DCB
又∵AB=DC，BC=BC
在△ABC和△DCB中，

AB=DC ∠ABC=∠DCB BC=BC

，
∴△ABC≌△DCB（SAS）
∴∠ACB=∠DBC     
又∵cos∠BGC=

1

2

∴∠BGC=60°
∴△BGC是等边三角形．

（2）解：连结ED．
∵同理可证△AGD也是等边三角形
又∵点E平分AG，
∴DE⊥AG
∴△DEC是直角三角形
又∵点F平分DC
∴DC=2EF=2×6=12．

点评：本题考查了全等三角形的判定、直角三角形的性质、等边三角形的性质等，作辅助线是本题的关键．