题目内容
3.杭州微公交公司有20辆微公交纯电动汽车(K10车型).单日租金120元/辆,可全部租出;“十一”黄金周期间,日租金每增加15元/辆,则多一辆车未能租出;公司平均每日的各项支出为1440元.设公司每日租出x辆车,日收益为y元.(日收益=日租金总收入-平均每日各项支出)(1)求每辆车的日租金(用含x的代数式表示);
(2)要使公司日收益最大,每日应租出多少辆?
(3)每日租出多少辆车时,公司的日收益既不盈利也不亏损?
分析 (1)由租出x辆汽车,就有(20-x)辆没有租出,每辆车的租金就增加15(20-x)元,就可以求出每辆车的日租金;
(2)根据日收益=日租金收入一平均每日各项支出,求出y与x之间的函数关系式,化为顶点式就可以求出结论;
(3)当y=0时建立一元二次方程求出其解即可.
解答 解:(1)根据题意,每辆车的日租金为120+15(20-x)=420-15x;
(2)由题意得:y=(420-15x)x-1440=-15x2+420x-1440=-15(x-14)2+1500,
即在0≤x≤20范围内,当x=14时,y有最大值
∴当每日租出14辆时,公司日收益最大;
(3)公司的日收益不盈利也不亏损,则y=0
即-15(x-14)2+1500=0
解得 x1=24,x2=4.
∵x=24不满足0≤x≤20,不合题意,舍去
∴x=4,
∴当每日租出4辆时,公司的日收益不盈利也不亏损.
点评 本题考查了代数式表示数的运用,二次函数的性质的运用,一元二次方程的解法的运用,日收益=日租金收入一平均每日各项支出的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
11.据调查,我市2013年的房屋均价为9680元/m2,到2015年下降到8000元/m2,求这两年的年平均下降率,设年平均下降率为x,根据题意,所列方程为( )
| A. | 9680(1-x)=8000 | B. | 9680(1+x2)=8000 | C. | 9680(1-2x)=4000 | D. | 9680(1-x)2=8000 |
15.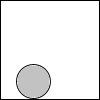 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )| A. | a2-π | B. | 4-π | C. | π | D. | (4-π)a2 |