题目内容
15.计算(1)($\sqrt{24}$-$\sqrt{2}$)-($\sqrt{8}$+$\sqrt{6}$);
(2)2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷$\sqrt{2}$;
(3)$\sqrt{18a}$-$\sqrt{\frac{1}{8}a}$+4$\sqrt{0.5a}$;
(4)$\sqrt{24}$(-$\sqrt{\frac{2}{3}}$+3$\sqrt{\frac{5}{6}}$+$\sqrt{5}$);
(5)(4+$\sqrt{5}$)(4-$\sqrt{5}$);
(6)($\sqrt{5}$-$\sqrt{3}$+$\sqrt{2}$)($\sqrt{5}$-$\sqrt{3}$-$\sqrt{2}$)
分析 (1)首先化简二次根式进而合并求出答案;
(2)直接利用二次根式乘除运算法则化简进而求出答案;
(3)首先化简二次根式进而合并求出答案;
(4)首先化简二次根式进而合并求出答案;
(5)直接利用平方差公式计算得出答案;
(6)直接利用平方差公式再结合完全平方公式计算得出答案.
解答 解:(1)($\sqrt{24}$-$\sqrt{2}$)-($\sqrt{8}$+$\sqrt{6}$)
=2$\sqrt{6}$-$\sqrt{2}$-2$\sqrt{2}$-$\sqrt{6}$
=$\sqrt{6}$-3$\sqrt{2}$;
(2)2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷$\sqrt{2}$
=4$\sqrt{3}$×$\frac{\sqrt{3}}{4}$÷$\sqrt{2}$
=3÷$\sqrt{2}$
=$\frac{3\sqrt{2}}{2}$;
(3)$\sqrt{18a}$-$\sqrt{\frac{1}{8}a}$+4$\sqrt{0.5a}$
=3$\sqrt{2a}$-$\frac{\sqrt{2a}}{4}$+4×$\frac{\sqrt{2a}}{2}$
=$\frac{19\sqrt{2a}}{4}$;
(4)$\sqrt{24}$(-$\sqrt{\frac{2}{3}}$+3$\sqrt{\frac{5}{6}}$+$\sqrt{5}$)
=2$\sqrt{6}$(-$\sqrt{\frac{2}{3}}$+3$\sqrt{\frac{5}{6}}$+$\sqrt{5}$)
=-2$\sqrt{6×\frac{2}{3}}$+6$\sqrt{6×\frac{5}{6}}$+2$\sqrt{30}$
=-4+6$\sqrt{5}$+2$\sqrt{30}$;
(5)(4+$\sqrt{5}$)(4-$\sqrt{5}$)
=16-5
=11;
(6)($\sqrt{5}$-$\sqrt{3}$+$\sqrt{2}$)($\sqrt{5}$-$\sqrt{3}$-$\sqrt{2}$)
=($\sqrt{5}$-$\sqrt{3}$)2-($\sqrt{2}$)2
=5+3-2$\sqrt{15}$-2
=6-2$\sqrt{15}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

 53随堂测系列答案
53随堂测系列答案| A. | 2a2-6a3=5a5 | B. | (x+y)2=x2+y2 | C. | a6÷a3=a2 | D. | (-a3)2=a6 |
| A. | 3 | B. | 5 | C. | 15 | D. | $\frac{3}{5}$ |
 “十一黄金周”期间,小明一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
“十一黄金周”期间,小明一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.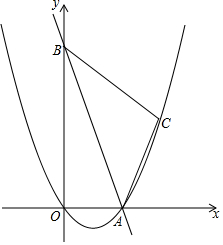 如图,在平面直角坐标系中,直线y=-2x+10与x轴、y轴相交于A、B两点,点C的坐标是(8,4),连接AC、BC.
如图,在平面直角坐标系中,直线y=-2x+10与x轴、y轴相交于A、B两点,点C的坐标是(8,4),连接AC、BC.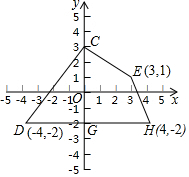 在平面直角坐标系中,四边形CDHE的位置如图所示,求四边形CDHE的面积.
在平面直角坐标系中,四边形CDHE的位置如图所示,求四边形CDHE的面积.