题目内容
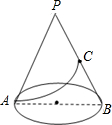 如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离.
如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离.考点:平面展开-最短路径问题,圆锥的计算
专题:
分析:最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.需先算出圆锥侧面展开图的扇形半径.看如何构成一个直角三角形,然后根据勾股定理进行计算.
解答: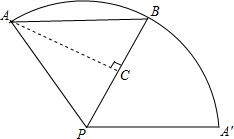 解:圆锥的底面周长是6π,则6π=
解:圆锥的底面周长是6π,则6π=
,
解得:n=120°,
即圆锥侧面展开图的圆心角是120度.
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90度.
∵在圆锥侧面展开图中AP=9,PC=
,
∴在圆锥侧面展开图中AC=
=
(cm).
故A点到 C点在圆锥的侧面上的最短距离为
cm.
 解:圆锥的底面周长是6π,则6π=
解:圆锥的底面周长是6π,则6π=| nπ×9 |
| 180 |
解得:n=120°,
即圆锥侧面展开图的圆心角是120度.
∴∠APB=60°,
∵PA=PB,
∴△PAB是等边三角形,
∵C是PB中点,
∴AC⊥PB,
∴∠ACP=90度.
∵在圆锥侧面展开图中AP=9,PC=
| 9 |
| 2 |
∴在圆锥侧面展开图中AC=
| AP2-PC2 |
9
| ||
| 2 |
故A点到 C点在圆锥的侧面上的最短距离为
9
| ||
| 2 |
点评:本题考查了圆锥的计算,需注意最短距离的问题最后都要转化为平面上两点间的距离的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
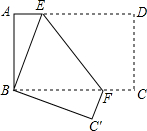 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′出,折痕为EF,
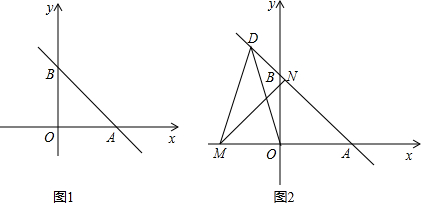
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′出,折痕为EF, 把下面的直线补充成一条数轴,然后在数轴上标出下列各数,并按从小到大的顺序用“<“连接起来.
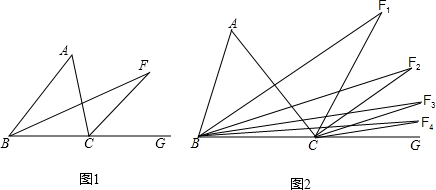
把下面的直线补充成一条数轴,然后在数轴上标出下列各数,并按从小到大的顺序用“<“连接起来. 如图,有甲、乙两建筑物,甲建筑物的高度为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.
如图,有甲、乙两建筑物,甲建筑物的高度为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC. 如图,M为弧AB的中点,MD⊥OA于D,ME⊥OB于E,求证:MD=ME.
如图,M为弧AB的中点,MD⊥OA于D,ME⊥OB于E,求证:MD=ME.