题目内容
(1)已知,如图1,BF为∠ABC的角平分线,CF为外角∠ACG的角平分线:
①若∠F=18°,求∠A= ;
②若∠A=n°,求∠F= ;(论证这个结论)
(2)如图2,若∠ABC与∠ACG的平分线交于F1;∠F1BC与∠F1CG的平分线交于F2;如此下去,∠F2BC与∠F2CG的平分线交于F3;试直接写出∠Fn与∠A的关系(n为自然数),不需要证明过程.
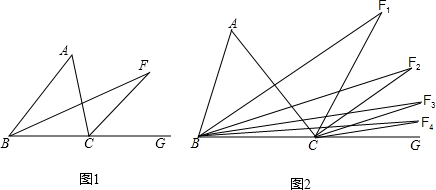
①若∠F=18°,求∠A=
②若∠A=n°,求∠F=
(2)如图2,若∠ABC与∠ACG的平分线交于F1;∠F1BC与∠F1CG的平分线交于F2;如此下去,∠F2BC与∠F2CG的平分线交于F3;试直接写出∠Fn与∠A的关系(n为自然数),不需要证明过程.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)由外角的性质可得∠FCG=∠F+∠FBC,∠ACG=∠ABC+∠A,再根据角平分线的定义可得到∠A=2∠F,进一步可求得∠A和∠F;
(2)同理可知∠A=2∠F1=4∠F2=…=2n∠Fn.
(2)同理可知∠A=2∠F1=4∠F2=…=2n∠Fn.
解答:解:(1)①在△FBC中,可得∠FCG=∠F+∠FBC,
∴2∠FCG=2∠F+2∠FBC,
在△ABC中,可得∠ACG=∠ABC+∠A,
∵BF为∠ABC的角平分线,CF为外角∠ACG的角平分线,
∴∠ACG=2∠FCG,∠ABC=2∠FBC,
∴2∠FCG=2∠FBC+∠A,
∴∠A=2∠F=2×18°=36°,
故答案为:36°;
②由①知∠A=2∠F,
∴∠F=
∠A=
,(论证过程同①)
故答案为:
;
(2)由①可知:∠A=2∠F1,
同理可知∠F1=2∠F2,∠F2=2∠F3,…,
∴∠A=2∠F1=4∠F2=…=2n∠Fn,
即∠A=2n∠Fn,
故答案为:∠A=2n∠Fn.
∴2∠FCG=2∠F+2∠FBC,
在△ABC中,可得∠ACG=∠ABC+∠A,
∵BF为∠ABC的角平分线,CF为外角∠ACG的角平分线,
∴∠ACG=2∠FCG,∠ABC=2∠FBC,
∴2∠FCG=2∠FBC+∠A,
∴∠A=2∠F=2×18°=36°,
故答案为:36°;
②由①知∠A=2∠F,
∴∠F=
| 1 |
| 2 |
| n° |
| 2 |
故答案为:
| n° |
| 2 |
(2)由①可知:∠A=2∠F1,
同理可知∠F1=2∠F2,∠F2=2∠F3,…,
∴∠A=2∠F1=4∠F2=…=2n∠Fn,
即∠A=2n∠Fn,
故答案为:∠A=2n∠Fn.
点评:本题主要考查三角形外角的性质及角平分线的定义,由条件得到∠A和∠F的关系是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
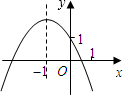 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a-b+c>1;③abc>0;④4a-2b+c<0;⑤c-a>1,其中所有正确结论的序号是( )
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a-b+c>1;③abc>0;④4a-2b+c<0;⑤c-a>1,其中所有正确结论的序号是( )| A、①②③⑤ | B、①③④ |
| C、①②③④ | D、①②③④⑤ |

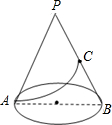 如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离.
如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离.