题目内容
 如图,M为弧AB的中点,MD⊥OA于D,ME⊥OB于E,求证:MD=ME.
如图,M为弧AB的中点,MD⊥OA于D,ME⊥OB于E,求证:MD=ME.考点:圆心角、弧、弦的关系,角平分线的性质
专题:证明题
分析:连接MO,根据等弧对等弦,则∠MOD=∠MOE,再由角平分线的性质,得出MD=ME.
解答: 证明:连接MO,
证明:连接MO,
∵
=
,
∴∠MOD=∠MOE,
又∵MD⊥OA于D,ME⊥OB于E,
∴MD=ME.
 证明:连接MO,
证明:连接MO,∵
 |
| AM |
 |
| MB |
∴∠MOD=∠MOE,
又∵MD⊥OA于D,ME⊥OB于E,
∴MD=ME.
点评:本题考查了等弧对等弦,以及角平分线的性质.关键是掌握角的平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目
经过平面上4个点中的每两个点画直线,最多可以画( )
| A、2条 | B、6条 | C、4条 | D、3条 |
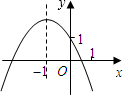 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a-b+c>1;③abc>0;④4a-2b+c<0;⑤c-a>1,其中所有正确结论的序号是( )
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a-b+c>1;③abc>0;④4a-2b+c<0;⑤c-a>1,其中所有正确结论的序号是( )| A、①②③⑤ | B、①③④ |
| C、①②③④ | D、①②③④⑤ |
已知等腰三角形的一边长为6,一个内角为60°,则它的周长是( )
| A、12 | B、15 | C、16 | D、18 |
现有一块长80cm、宽60cm的矩形钢片,将它的四个角各剪去一个边长为x cm的小正方形,做成一个底面积为y cm2的无盖的长方体盒子,则y与x之间的函数关系式为( )
| A、y=x2-70x+1200 |
| B、y=x2-140x+4800 |
| C、y=4x2-280x+4800 |
| D、y=4800-4x2 |
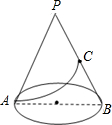 如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离.
如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离. 如图是拉线固定电线杆的示意图.点A、D、B在同一直线上.已知CD⊥AB,CD=3
如图是拉线固定电线杆的示意图.点A、D、B在同一直线上.已知CD⊥AB,CD=3