题目内容
如图1,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a,b满足
+(3-b)2=0;
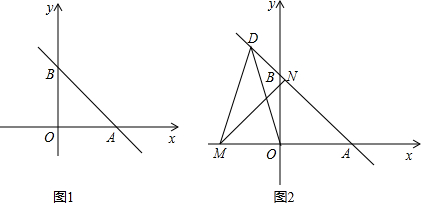
(1)求A,B的坐标;
(2)求∠OBA的度数;
(3)如图2,在第二象限内的直线AB上有一动点D,在x轴的负半轴上一点M,满足DM=DO若MN⊥AB于N,请判断线段AB与DN的数量关系,并说明理由.
| a-3 |

(1)求A,B的坐标;
(2)求∠OBA的度数;
(3)如图2,在第二象限内的直线AB上有一动点D,在x轴的负半轴上一点M,满足DM=DO若MN⊥AB于N,请判断线段AB与DN的数量关系,并说明理由.
考点:全等三角形的判定与性质,勾股定理的应用
专题:计算题
分析:(1)根据平方根和平方数均≥0可解题;
(2)OA=OB,即可判定△AOB为等腰直角三角形;
(3)在平面直角坐标系中求出点D,N的坐标即可求得DN的长度,即可解题.
(2)OA=OB,即可判定△AOB为等腰直角三角形;
(3)在平面直角坐标系中求出点D,N的坐标即可求得DN的长度,即可解题.
解答:解:(1)∵
+(3-b)2=0,
∴a=b=3,
∴A(3,0),B(0,3);
(2)∵OA=OB=3,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴∠OBA=45°;
(3)直线AB解析式为y=-x+3,
设D点坐标(a,3-a),则M点坐标为(2a,0),
∵直线MN⊥AB,且过M点,
∴直线MN的坐标为y=x-2a,
∴N点坐标为(a+
,
-a),
∴DN2=(
)2+(
)2,
∴DN=
,
∵AB=3
,
∴AB=2DN.
| a-3 |
∴a=b=3,
∴A(3,0),B(0,3);
(2)∵OA=OB=3,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴∠OBA=45°;
(3)直线AB解析式为y=-x+3,
设D点坐标(a,3-a),则M点坐标为(2a,0),
∵直线MN⊥AB,且过M点,
∴直线MN的坐标为y=x-2a,
∴N点坐标为(a+
| 3 |
| 2 |
| 3 |
| 2 |
∴DN2=(
| 3 |
| 2 |
| 3 |
| 2 |
∴DN=
| 3 |
| 2 |
| 2 |
∵AB=3
| 2 |
∴AB=2DN.
点评:此题考查了平面直角坐标系中线段长的求值,熟练运用平面直角坐标系坐标是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图,在公路L的一侧有A、B两个村庄,A、B到公路的距离AE和BD分别为300米和480米,且DE为1300米,现要在公路边建一供水站C,向两村庄供水,且使水管最短.
如图,在公路L的一侧有A、B两个村庄,A、B到公路的距离AE和BD分别为300米和480米,且DE为1300米,现要在公路边建一供水站C,向两村庄供水,且使水管最短.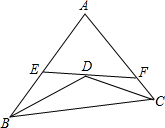 如图,BD,CD分别平分∠ABC,∠ACB,过点D作直线分别交AB,AC于点E,F,若AE=AF,BE=4,CF=2,则EF的长为( )
如图,BD,CD分别平分∠ABC,∠ACB,过点D作直线分别交AB,AC于点E,F,若AE=AF,BE=4,CF=2,则EF的长为( )
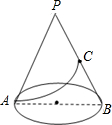 如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离.
如图,已知圆锥的底面半径为3,母线长为9,C为母线PB的中点,求从A点到 C点在圆锥的侧面上的最短距离. 如图是拉线固定电线杆的示意图.点A、D、B在同一直线上.已知CD⊥AB,CD=3
如图是拉线固定电线杆的示意图.点A、D、B在同一直线上.已知CD⊥AB,CD=3