题目内容
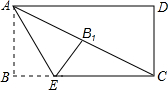 如图,在矩形纸片ABCD中,AB=1,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=
如图,在矩形纸片ABCD中,AB=1,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=考点:翻折变换(折叠问题)
专题:计算题
分析:先根据矩形的性质得∠B=90°,再根据折叠的性质得到AB1=AB=1,∠AB1E=∠B=90°,则EB1⊥AC,由于AE=CE,根据等腰三角形的性质可得到AB1=CB1=1,所以AC=2AB1=2.
解答:解:∵四边形ABCD为矩形,
∴∠B=90°,
∵将纸片沿AE折叠,点B恰好与AC上的点B1重合,
∴AB1=AB=1,∠AB1E=∠B=90°,
∴EB1⊥AC,
而AE=CE,
∴AB1=CB1=1,
∴AC=2AB1=2.
故答案为2.
∴∠B=90°,
∵将纸片沿AE折叠,点B恰好与AC上的点B1重合,
∴AB1=AB=1,∠AB1E=∠B=90°,
∴EB1⊥AC,
而AE=CE,
∴AB1=CB1=1,
∴AC=2AB1=2.
故答案为2.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和等腰三角形的性质.

练习册系列答案
相关题目
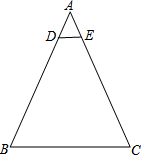 如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD:DB=1:4,S△ADE=4,则S△ABC=( )
如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD:DB=1:4,S△ADE=4,则S△ABC=( )| A、4 | B、16 | C、25 | D、100 |
 在平面直角坐标系中,已知点B(a,b),线段BA⊥x轴于A点,线段BC⊥y轴于C点,且(a-b+2)2+|2a-b-2|=0.
在平面直角坐标系中,已知点B(a,b),线段BA⊥x轴于A点,线段BC⊥y轴于C点,且(a-b+2)2+|2a-b-2|=0. 如图,在△ABC中,∠C=90°,∠B=30°,D为AB的中点,则∠DCB=
如图,在△ABC中,∠C=90°,∠B=30°,D为AB的中点,则∠DCB=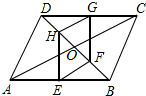 如图,平行四边形ABCD中,AC、BD相交于点O,E、F、G、H分别是AB、OB、CD、OD的中点.有下列结论:①AD=BC,②△DHG≌△BFE,③BF=HO,④AO=BO,⑤四边形HFEG是平行四边形,其中正确结论的序号是
如图,平行四边形ABCD中,AC、BD相交于点O,E、F、G、H分别是AB、OB、CD、OD的中点.有下列结论:①AD=BC,②△DHG≌△BFE,③BF=HO,④AO=BO,⑤四边形HFEG是平行四边形,其中正确结论的序号是