题目内容
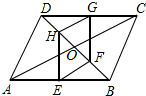 如图,平行四边形ABCD中,AC、BD相交于点O,E、F、G、H分别是AB、OB、CD、OD的中点.有下列结论:①AD=BC,②△DHG≌△BFE,③BF=HO,④AO=BO,⑤四边形HFEG是平行四边形,其中正确结论的序号是
如图,平行四边形ABCD中,AC、BD相交于点O,E、F、G、H分别是AB、OB、CD、OD的中点.有下列结论:①AD=BC,②△DHG≌△BFE,③BF=HO,④AO=BO,⑤四边形HFEG是平行四边形,其中正确结论的序号是考点:平行四边形的判定与性质,全等三角形的判定与性质
专题:
分析:根据平行四边形的性质,可判定①;
根据平行四边形的性质,可得OD与OB的关系,AB与DC的关系,根据全等三角形的判定,可判断②;
根据全等三角形的性质,可得BF与DH的关系,根据等量代换,可得③答案;
根据平行四边形的性质,可得④的答案;
根据平行四边形的判定,可得⑤的答案.
根据平行四边形的性质,可得OD与OB的关系,AB与DC的关系,根据全等三角形的判定,可判断②;
根据全等三角形的性质,可得BF与DH的关系,根据等量代换,可得③答案;
根据平行四边形的性质,可得④的答案;
根据平行四边形的判定,可得⑤的答案.
解答:解:平行四边形ABCD中,
∴AD=BC,故①正确;
∵平行四边形ABCD,
∴DC∥AB,DC=AB,OD=OB,
∴∠CDB=∠DBA,
∵E、F、G、H分别是AB、OB、CD、OD的中点,
∴DG=BE=
AB,DH=BF=
OD,
∴②△DHG≌△BFE,故②正确;
∵HO=DH,DH=BF,
∴BF=HO,故③正确;
平行四边形ABCD,OA=OC,OB=OD,故④错误;
E、F、G、H分别是AB、OB、CD、OD的中点,
∴HG∥OC,HG=
OC,EF∥OA,EF=
OA,
∴HG∥EF,HG=EF,
HEFG是平行四边形,故⑤正确;
故答案为:①,②,③,⑤.
∴AD=BC,故①正确;
∵平行四边形ABCD,
∴DC∥AB,DC=AB,OD=OB,
∴∠CDB=∠DBA,
∵E、F、G、H分别是AB、OB、CD、OD的中点,
∴DG=BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴②△DHG≌△BFE,故②正确;
∵HO=DH,DH=BF,
∴BF=HO,故③正确;
平行四边形ABCD,OA=OC,OB=OD,故④错误;
E、F、G、H分别是AB、OB、CD、OD的中点,
∴HG∥OC,HG=
| 1 |
| 2 |
| 1 |
| 2 |
∴HG∥EF,HG=EF,
HEFG是平行四边形,故⑤正确;
故答案为:①,②,③,⑤.
点评:本题考查了平行四边形的判定与性质,利用了平行四边形的判定与性质,三角形的中位线,全等三角形的判定.

练习册系列答案
相关题目
下列各数中,无理数的个数有( )
;3π;
;-2.
;
;
;0.323323332…;2-
;
,(-3
)2.
| 2 |
| 3 | 8 |
| • |
| 1 |
| 22 |
| 7 |
| 0.9 |
| 3 |
| (-4)3 |
| 2 |
| A、3个 | B、4个 | C、5个 | D、6个 |
 如图,已知BC是以AB为直径的⊙的切线,且BC=AB,连接OC交⊙O于点D,延长AD交BC于点E,F为BE上一点,且DF=FB.
如图,已知BC是以AB为直径的⊙的切线,且BC=AB,连接OC交⊙O于点D,延长AD交BC于点E,F为BE上一点,且DF=FB.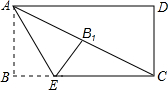 如图,在矩形纸片ABCD中,AB=1,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=
如图,在矩形纸片ABCD中,AB=1,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=