题目内容
 在平面直角坐标系中,已知点B(a,b),线段BA⊥x轴于A点,线段BC⊥y轴于C点,且(a-b+2)2+|2a-b-2|=0.
在平面直角坐标系中,已知点B(a,b),线段BA⊥x轴于A点,线段BC⊥y轴于C点,且(a-b+2)2+|2a-b-2|=0.(1)求A,B,C三点的坐标;
(2)若点D是AB的中点,点E是OD的中点,求△AEC的面积;
(3)在(2)的条件下,若已知点P(2,a),且S△AEP=S△AEC,求a的值.
考点:坐标与图形性质,三角形的面积
专题:计算题
分析:(1)根据非负数的性质得a-b+2=0,2a-b-2=0,解得a=4,b=6,则B点坐标为(4,6),由于线段BA⊥x轴于A点,线段BC⊥y轴于C点,易得A点坐标为(4,0),C点坐标为(0,6);
(2)利用线段中点坐标公式得到点D的坐标为(4,3),点E的坐标为(2,
),再根据三角形面积公式和S△AEC=S△AOC-S△AOE-S△COE进行计算;
(3)由于点P(2,a),点E的坐标为(2,
),则PE=|a-
|,由于S△AEP=S△AEC,根据三角形面积公式
•2•|a-
|=3,然后去绝对值可计算出a的值.
(2)利用线段中点坐标公式得到点D的坐标为(4,3),点E的坐标为(2,
| 3 |
| 2 |
(3)由于点P(2,a),点E的坐标为(2,
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:(1)∵(a-b+2)2+|2a-b-2|=0,
∴a-b+2=0,2a-b-2=0,
∴a=4,b=6,
∴B点坐标为(4,6),
∵线段BA⊥x轴于A点,线段BC⊥y轴于C点,
∴A点坐标为(4,0),C点坐标为(0,6);
(2)∵点D是AB的中点,
∴点D的坐标为(4,3),
∵点E是OD的中点,
∴点E的坐标为(2,
),
∴S△AEC=S△AOC-S△AOE-S△COE
=
×6×4-
×4×
-
×6×2
=3;
(3)∵点P(2,a),点E的坐标为(2,
),
∴PE=|a-
|,
∵S△AEP=S△AEC,
∴
•2•|a-
|=3,
∴a=-
或
.
∴a-b+2=0,2a-b-2=0,
∴a=4,b=6,
∴B点坐标为(4,6),
∵线段BA⊥x轴于A点,线段BC⊥y轴于C点,
∴A点坐标为(4,0),C点坐标为(0,6);
(2)∵点D是AB的中点,
∴点D的坐标为(4,3),
∵点E是OD的中点,
∴点E的坐标为(2,
| 3 |
| 2 |
∴S△AEC=S△AOC-S△AOE-S△COE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
=3;
(3)∵点P(2,a),点E的坐标为(2,
| 3 |
| 2 |
∴PE=|a-
| 3 |
| 2 |
∵S△AEP=S△AEC,
∴
| 1 |
| 2 |
| 3 |
| 2 |
∴a=-
| 3 |
| 2 |
| 9 |
| 2 |
点评:本题考查了坐标与图形性质:能根据点的坐标表示它到两坐标轴的距离,记住坐标轴上点的坐标特征.也考查了三角形的面积公式.

练习册系列答案
相关题目
 如图,已知BC是以AB为直径的⊙的切线,且BC=AB,连接OC交⊙O于点D,延长AD交BC于点E,F为BE上一点,且DF=FB.
如图,已知BC是以AB为直径的⊙的切线,且BC=AB,连接OC交⊙O于点D,延长AD交BC于点E,F为BE上一点,且DF=FB.
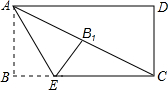 如图,在矩形纸片ABCD中,AB=1,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=
如图,在矩形纸片ABCD中,AB=1,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=