题目内容
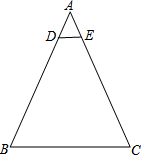 如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD:DB=1:4,S△ADE=4,则S△ABC=( )
如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,AD:DB=1:4,S△ADE=4,则S△ABC=( )| A、4 | B、16 | C、25 | D、100 |
考点:相似三角形的判定与性质
专题:
分析:由DE∥BC,所以△ADE∽△ABC,根据相似三角形的对应边对应成比例可求出解.
解答:解:∵∠ADE=∠B=80°,
∴DE∥BC,
∴△ADE∽△ABC,
∵AD:DB=1:4,
∴AD:AB=1:5 S△ADE:S△ABC=1:25,
又∵S△ADE=4,
∴S△ABC=100,
故选:D.
∴DE∥BC,
∴△ADE∽△ABC,
∵AD:DB=1:4,
∴AD:AB=1:5 S△ADE:S△ABC=1:25,
又∵S△ADE=4,
∴S△ABC=100,
故选:D.
点评:本题考查相似三角形的判定和性质,关键是知道相似三角形的对应边对应成比例.

练习册系列答案
相关题目
方程
-
=1的解是( )
| 2x+1 |
| x-1 |
| 2 |
| x-1 |
| A、x=0 | B、x=-1 |
| C、x=1 | D、无解 |
 ∠BAC放在正方形网格纸的位置如图,则tan∠BAC的值为( )
∠BAC放在正方形网格纸的位置如图,则tan∠BAC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在等腰梯形ABCD中,AD∥BC,∠B=70°,DE∥AB,将△DCE沿DE翻折,得到△DC′E,则∠EDC′=( )
如图,在等腰梯形ABCD中,AD∥BC,∠B=70°,DE∥AB,将△DCE沿DE翻折,得到△DC′E,则∠EDC′=( )| A、30° | B、40° |
| C、55° | D、70° |
下列各数中,无理数的个数有( )
;3π;
;-2.
;
;
;0.323323332…;2-
;
,(-3
)2.
| 2 |
| 3 | 8 |
| • |
| 1 |
| 22 |
| 7 |
| 0.9 |
| 3 |
| (-4)3 |
| 2 |
| A、3个 | B、4个 | C、5个 | D、6个 |
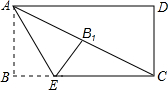 如图,在矩形纸片ABCD中,AB=1,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=
如图,在矩形纸片ABCD中,AB=1,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=