题目内容
 “锤子、剪刀、布”是一个古老的儿童游戏,三种不同手势分别代表锤子、剪刀、布.规则是:锤子胜剪刀,剪刀胜布,布胜锤子;当两人做出相同的手势时,不能决定胜负.设甲、乙两人都等可能地采取三种手势.
“锤子、剪刀、布”是一个古老的儿童游戏,三种不同手势分别代表锤子、剪刀、布.规则是:锤子胜剪刀,剪刀胜布,布胜锤子;当两人做出相同的手势时,不能决定胜负.设甲、乙两人都等可能地采取三种手势.(1)求一个回合不能决定胜负的概率.
(2)分别求甲、乙获胜的概率.
(3)用这种方式决定胜负公平吗?
考点:游戏公平性,列表法与树状图法
专题:
分析:(1)首先画出树形图,根据游戏规则即可求出一个回合不能决定胜负的概率.
(2)由(1)树形图即可求出甲、乙获胜的概率.
(3)用这种方式决定胜负公平,由(2)可知题目获胜的概率相等.
(2)由(1)树形图即可求出甲、乙获胜的概率.
(3)用这种方式决定胜负公平,由(2)可知题目获胜的概率相等.
解答:解:(1)根据题意,有
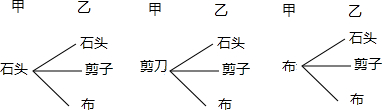
分析可得,共9种情况,两人一次性分不出胜负的有3种;故其概率为
=
;
(2)甲胜的情况为(石头,剪子),(剪子,布),(布,石头)三种情况,
所以甲胜的概率为P(A)=
;
乙胜的情况为(石头,剪子),(剪子,布),(布,石头)三种情况,
所以乙胜的概率为P(B)=
;
(3)用这种方式决定胜负公平,因为P甲获胜=P乙获胜.

分析可得,共9种情况,两人一次性分不出胜负的有3种;故其概率为
| 3 |
| 9 |
| 1 |
| 3 |
(2)甲胜的情况为(石头,剪子),(剪子,布),(布,石头)三种情况,
所以甲胜的概率为P(A)=
| 1 |
| 3 |
乙胜的情况为(石头,剪子),(剪子,布),(布,石头)三种情况,
所以乙胜的概率为P(B)=
| 1 |
| 3 |
(3)用这种方式决定胜负公平,因为P甲获胜=P乙获胜.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.游戏双方获胜的概率相同,游戏就公平,否则游戏不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,直线y=kx+b与双曲线y=
如图,直线y=kx+b与双曲线y= 如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=140°,∠E=80°,试求∠F的度数.
如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=140°,∠E=80°,试求∠F的度数.
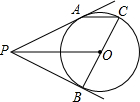 如图,PA、PB分别切⊙O于A、B,BC为⊙O的直径.
如图,PA、PB分别切⊙O于A、B,BC为⊙O的直径.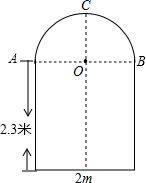 一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状为如图所示的某工厂,厂门上部为半圆形,下部为长方形,已知长方形的宽为2米,高为2.3米,半圆形的直径与门的宽相等.问这辆卡车能否通过该工厂的厂门?
一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状为如图所示的某工厂,厂门上部为半圆形,下部为长方形,已知长方形的宽为2米,高为2.3米,半圆形的直径与门的宽相等.问这辆卡车能否通过该工厂的厂门?