题目内容
15．计算：$\sqrt{12}$-|$\sqrt{3}$-2|+（2016-2$\sqrt{3}$）0-4cos60°+（$\frac{1}{3}$）-1．分析 根据实数的运算，即可解答．
解答 解：原式=2$\sqrt{3}$-（2-$\sqrt{3}$）+1-4×$\frac{1}{2}$+3
=2$\sqrt{3}$-2+$\sqrt{3}$+1-2+3
=3$\sqrt{3}$．
点评 本题考查了实数的运算，解决本题的关键是熟记实数的运算．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
5．已知：（a-b）2=9；（a+b）2=25，则a2+b2=（ ）
| A． | 34 | B． | 16 | C． | -16 | D． | 17 |
实数a、b在数轴上的位置如图所示，则化简 $\sqrt{{{（-a）}^2}}+\sqrt{b^2}-\sqrt{{{（a+b）}^2}}$的结果为2b．
10．八年级学生去距学校11km的科技馆参观，一部分学生骑自行车，过了20min后，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度，设骑车学生的速度为xkm/h，则所列方程正确的是（ ）
| A． | $\frac{11}{x}=\frac{11}{2x}-\frac{1}{3}$ | B． | $\frac{11}{x}=\frac{11}{2x}-20$ | C． | $\frac{11}{x}=\frac{11}{2x}+\frac{1}{3}$ | D． | $\frac{11}{x}=\frac{11}{2x}+20$ |
20．九（1）班第5学习小组共有2位女生和3位男生．一次数学课上，老师随机让该学习小组的2位同学上台演示解题过程（每个同学上台演示的可能性相同），则上台演示解题过程的2位同学都是女生的概率等于（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{1}{10}$ | C． | $\frac{4}{25}$ | D． | $\frac{1}{2}$ |
3．
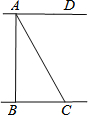如图，河岸AD、BC互相平行，桥AB垂直于两岸，从C处看桥的两端A、B，夹角∠BCA=50度，测得BC=45m，则桥长AB=（ ）m．
如图，河岸AD、BC互相平行，桥AB垂直于两岸，从C处看桥的两端A、B，夹角∠BCA=50度，测得BC=45m，则桥长AB=（ ）m．| A． | $\frac{45}{cos50°}$ | B． | 45•cos50° | C． | $\frac{45}{tan50°}$ | D． | 45•tan50° |
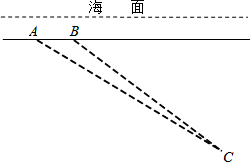如图，一艘潜艇在海面下500m深的点A处，测得正前方俯角为31°方向上的海底有黑匣子发出信号，潜艇在同一深度保持直线航行500m，在点B处测得海底黑匣子位于正前方俯角36.9°的方向上，海底黑匣子C所在点距海面的深度为2000m．（精确到1，m．参考数据：sin36.9°≈0.60，cos36.9°≈0.80，tan36.9°≈0.75，sin31°≈0.51，cos31°≈0.87，tan31°≈0.60）