题目内容
19.某高科技发展公司投资500万元,成功研制出一种市场需求量较大的产品,并投入资金1500万元进行批量生产.已知生产每件产品的成本为40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量减少1万件.(1)计算销售单价为160元时的年获利,并说明同样的年获利,销售单价还可以定为多少元?
(2)公司计划在第一年按年获利最大确定的销售单价进行销售;第二年获利不低于1130万元,请说明第一年单价和第二年单价的范围.
分析 (1)由题意易得Z与x之间的函数关系,当x=160时则可推出x2-340x+28800=0,解得x的值.再分别把x的两个值代入y与x的函数关系式即可.
(2)把z与x的关系式化简,得出当x=170时,z取最大值.
解答 解:(1)设销售单价为x元时,年获利y万元,则$y=(30-\frac{x}{10})(x-40)-500-1500=-\frac{1}{10}{x^2}+34x-3200$,
当$x=160时,z=-\frac{1}{10}×{160^2}+34×160-3200=-320$,
令$-320=-\frac{1}{10}{x^2}+34x-3200$,
整理,得x2-340x+28800=0,
由根与系数的关系得x=180,即同样的年获利,销售单价还可以定为180元,
(2)∵$z=-\frac{1}{10}{x^2}+34x-3200=-\frac{1}{10}{(x-170)^2}-310$
∴当x=170时,z取最大值,最大值为-310
故第一年的销售单价定为170元/件,
∴当z=1130时,即$1130=-\frac{1}{10}{x^2}+34x-1510$,
整理得x2-340x+26400=0,
解得:x1=120,x2=220.
函数z=-$\frac{1}{10}$x2+34x-1510的图象大致如图所示: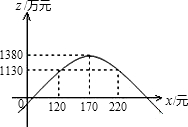
由图象可以看出:当120≤x≤220时,z≥1130.
故第二年销售量单价应确定在不低于120元且不高于220元的范围.
点评 本题考查的是二次函数在实际生活中的应用,解题时首先正确理解题意,然后利用已知条件列出方程或二次函数,然后解方程或利用二次函数的性质即可解决问题.

练习册系列答案
相关题目
14.下列函数中,y是x的一次函数的是y=3x;y=3+4x;2y=3x-4;2x+5y=0.6.
y=3x;y=3+4x;y=$\frac{1}{2}$;2y=3x-4;xy=3;2x+5y=0.6.
y=3x;y=3+4x;y=$\frac{1}{2}$;2y=3x-4;xy=3;2x+5y=0.6.
4.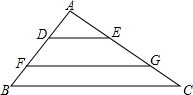 如图所示,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形BCGF,则DE:BC等于( )
如图所示,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形BCGF,则DE:BC等于( )
 如图所示,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形BCGF,则DE:BC等于( )
如图所示,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形BCGF,则DE:BC等于( )| A. | 1:2 | B. | 1:4 | C. | 1:$\sqrt{3}$ | D. | 1:$\sqrt{2}$ |
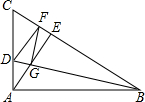 在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.
在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.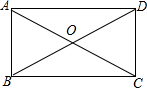 如图,矩形的两条对角线夹角为60°,一条短边为2,则矩形的长边长为2$\sqrt{3}$,对角线长为4.
如图,矩形的两条对角线夹角为60°,一条短边为2,则矩形的长边长为2$\sqrt{3}$,对角线长为4. 如图,已知圆锥的底面半径为5,侧面积为65π,则圆锥的高12.
如图,已知圆锥的底面半径为5,侧面积为65π,则圆锥的高12.