题目内容
计算:
+(
+
)+(
+
+
)+…+(
+
+
+…+
).
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 4 |
| 3 |
| 4 |
| 1 |
| 80 |
| 2 |
| 80 |
| 3 |
| 80 |
| 79 |
| 80 |
考点:有理数的加法
专题:
分析:根据计算,可发现规律:an=
+
+…+
=
,再根据有理数的加法,可得答案.
| 1 |
| n+1 |
| 2 |
| n+1 |
| n |
| n+1 |
| n |
| 2 |
解答:解:
+
=
=
,
+
+
=
=
,
+
+
+
=
=
,
发现规律:an=
+
+…+
=
=
=
,
∴原式=
+
+
+
+…+
=
=
=25×99
=25×(100-1)
=2475.
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 2 |
| 1 |
| 4 |
| 2 |
| 4 |
| 3 |
| 4 |
| 6 |
| 4 |
| 3 |
| 2 |
| 1 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 10 |
| 5 |
| 4 |
| 2 |
发现规律:an=
| 1 |
| n+1 |
| 2 |
| n+1 |
| n |
| n+1 |
=
| 1+2+3+…+n |
| n+1 |
=
| n(n+1) |
| 2(n+1) |
=
| n |
| 2 |
∴原式=
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| 4 |
| 2 |
| 99 |
| 2 |
=
| 1+2+3+…+99 |
| 2 |
=
| 99(1+99) |
| 2×2 |
=25×99
=25×(100-1)
=2475.
点评:本题考查了有理数的加法,发现规律是解题关键.

练习册系列答案
相关题目
在代数式:a,
(a+b)h,3.14k2,
,
,
,中,单项式的个数为( )
| 1 |
| 2 |
| 1 |
| a |
| 3x-1 |
| 2 |
| 1 |
| π |
| A、1个 | B、2个 | C、3个 | D、4个 |
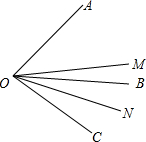 如图,已知
如图,已知