题目内容
2．掷一枚质地均匀的正方体骰子，骰子的六个面上的点数分别为1到6的整数，那么掷出的点数小于3的概率为$\frac{1}{3}$．分析 点数小于3的有2种情况，除以总个数6即为向上的一面的点数小于3的概率．
解答 解：∵共有6种情况，点数小于3的有2种，
∴P（点数小于3）=$\frac{2}{6}=\frac{1}{3}$．
故答案为$\frac{1}{3}$
点评 本题考查的是概率的求法的运用．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．
练习册系列答案
相关题目
13．用配方法解方程3x2-$\frac{12}{5}$x-1=0时，变形正确的是（ ）
| A． | （x+$\frac{2}{5}$）2-$\frac{37}{25}$=0 | B． | 3（x+$\frac{2}{5}$）2-$\frac{37}{25}$=0 | C． | （x-$\frac{2}{5}$）2-$\frac{37}{25}$=0 | D． | 3（x-$\frac{2}{5}$）2-$\frac{37}{25}$=0 |
10．在八边形内任取一点，把这个点与八边形各顶点分别连接可得到几个三角形（ ）
| A． | 5个 | B． | 6个 | C． | 7个 | D． | 8个 |
17．
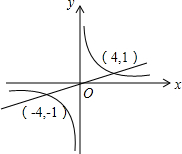如图，直线y=$\frac{1}{4}$x与双曲线y=$\frac{4}{x}$相交于（-4，-1）和（4，1），则不等式$\frac{1}{4}$x＞$\frac{4}{x}$的解集为（ ）
如图，直线y=$\frac{1}{4}$x与双曲线y=$\frac{4}{x}$相交于（-4，-1）和（4，1），则不等式$\frac{1}{4}$x＞$\frac{4}{x}$的解集为（ ）| A． | -4＜x＜0或x＞4 | B． | -4＞x或0＜x＜4 | C． | -4＜x＜4且x≠0 | D． | x＜-4或x＞4 |