题目内容
2．解方程（1）（x-2）2=3（x-2）．
（2）x2-5x-4=0．
分析 （1）因式分解法求解可得；
（2）公式法求解可得．
解答 解：（1）∵（x-2）2-3（x-2）=0，
∴（x-2）（x-5）=0，
∴x1=2，x2=5；
（2）∵a=1，b=-5，c=-4，
∴b2-4ac=（-5）2-4×1×（-4）=41，
∴${x_1}=\frac{{5+\sqrt{41}}}{2}$，$x{\;}_2=\frac{{5-\sqrt{41}}}{2}$．
点评 本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，四边形ABCD是平行四边形，E为边CD延长线上一点，连接BE交边AD于点F．请找出一对相似三角形，并加以证明．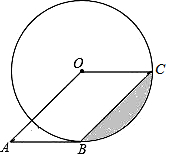
如图，四边形OABC为平行四边形，B、C在⊙O上，A在⊙O外，sin∠OCB=$\frac{\sqrt{2}}{2}$．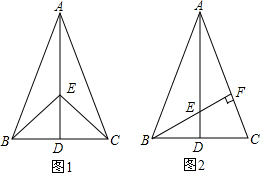
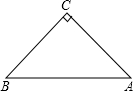△ABC是等腰直角三角形，其中∠C=90°，AC=BC，D是BC上任意一点（点D与点B、C都不重合），连接AD，CF⊥AD，交AD于点E，交AB于点F，BG⊥BC交CF的延长线于点G．
16．下列说法不正确的是（ ）
| A． | 3是9的平方根 | B． | 无理数都是无限小数 | ||
| C． | （3-π）2的算术平方根是3-π | D． | 实数与数轴上的点是一一对应的 |