题目内容
11．顺次连接四边形ABCD的各边中点所得的四边形是（ ）| A． | 矩形 | B． | 菱形 | C． | 平行四边形 | D． | 正方形 |
分析 连接原四边形的一条对角线，根据中位线定理，可得新四边形的一组对边平行且等于对角线的一半，即一组对边平行且相等．则新四边形是平行四边形；
解答 
解：（如图）根据中位线定理可得：GF=$\frac{1}{2}$BD且GF∥BD，EH=$\frac{1}{2}$BD且EH∥BD，
∴EH=FG，EH∥FG，
∴四边形EFGH是平行四边形．
故选C．
点评 此题主要考查学生对平行四边形的判定的掌握情况，综合利用了中位线定理，难度不大．
练习册系列答案
相关题目
如图，直线AB、CD被直线EF所截，当满足条件∠1=∠5时（只需写出一个你认为合适的条件），AB∥CD．
2．如图1，有两个全等的正三角形ABC和ODE，点O、C分别为△ABC、△ODE的重心；固定点O，将△ODE顺时针旋转，使得OD经过点C，如图2所示，则图2中四边形OGCF与△OCH面积的比为（ ）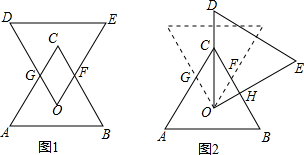
| A． | 1：1 | B． | 2：1 | C． | 4：1 | D． | 4：3 |
19．化简$\frac{{x}^{2}}{x-1}$+$\frac{x}{1-x}$的结果是（ ）
| A． | x+2 | B． | x-1 | C． | -x | D． | x |
如图，在平行四边形ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．证明：FD=AB．