题目内容
15.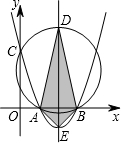 如图,开口向上的抛物线y=$\frac{1}{a}$(x-a)(x-3a)的顶点为E,与x轴相交于点A、B两点,与y轴交于点C,经过A、B、C三点的圆与抛物线的对称轴在x轴上方的交点为D.已知圆的半径是$3\sqrt{5}$,则四边形AEBD的面积是27+9$\sqrt{5}$.
如图,开口向上的抛物线y=$\frac{1}{a}$(x-a)(x-3a)的顶点为E,与x轴相交于点A、B两点,与y轴交于点C,经过A、B、C三点的圆与抛物线的对称轴在x轴上方的交点为D.已知圆的半径是$3\sqrt{5}$,则四边形AEBD的面积是27+9$\sqrt{5}$.
分析 由题意A(a,0),B(3a,0),C(0,3a),对称轴x=2a,顶点E(2a,-a),由OC=OB,O′C=O′B,推出点O′在直线y=x上,推出O′(2a,2a),在Rt△AO′F中,根据AO′2=AF2+O′F2,列出方程求出a,即可解决问题.
解答 解:如图,设圆心为O′,DE与AB交于点F.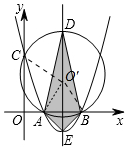
由题意A(a,0),B(3a,0),C(0,3a),
∴对称轴x=2a,顶点E(2a,-a),
∵OC=OB,O′C=O′B,
∴点O′在直线y=x上,
∴O′(2a,2a),
在Rt△AO′F中,∵AO′2=AF2+O′F2,
∴45=a2+(2a)2,
∵a>0,
∴a=3,
∴A(3,0),B(9,0),E(6,-3),D(6,6+3$\sqrt{5}$),
∴四边形AEBD的面积=$\frac{1}{2}$•AB•DE=$\frac{1}{2}$×6(6+3$\sqrt{5}$+3)=27+9$\sqrt{5}$.
故答案为27+9$\sqrt{5}$.
点评 本题考查抛物线与x轴的交点、三角形的外接圆、四边形的面积等知识,解题的关键是学会利用参数,构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
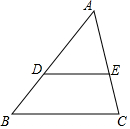 如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,DB=2,则$\frac{DE}{BC}$的值等于$\frac{3}{5}$.
如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,DB=2,则$\frac{DE}{BC}$的值等于$\frac{3}{5}$. 图象过点A(0,3)B(2,4).题目中的矩形部分是一段因墨水污染而无法辨认的文字.
图象过点A(0,3)B(2,4).题目中的矩形部分是一段因墨水污染而无法辨认的文字. 已知:∠α,∠β.请你用直尺和圆规作一个∠BAC,使∠BAC=∠α+∠β.(要求:要保留作图痕迹)
已知:∠α,∠β.请你用直尺和圆规作一个∠BAC,使∠BAC=∠α+∠β.(要求:要保留作图痕迹)