题目内容
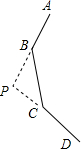 如图为一个正n边形的一部分,AB和DC延长后相交于点P,若∠BPC=120°,求n.
如图为一个正n边形的一部分,AB和DC延长后相交于点P,若∠BPC=120°,求n.考点:多边形内角与外角
专题:
分析:先根据等腰三角形的性质及三角形内角和定理求出∠PBC=∠PCB=30°,再根据多边形外角和为360°即可求解.
解答:解:∵PB=PC,∠BPC=120°,
∴∠PBC=∠PCB=
(180°-∠BPC)=30°,
即正n边形的一个外角为30°,
∴n=
=12.
∴∠PBC=∠PCB=
| 1 |
| 2 |
即正n边形的一个外角为30°,
∴n=
| 360° |
| 30° |
点评:本题考查了等腰三角形的性质,三角形内角和定理,多边形外角和定理,求出正n边形的一个外角为30°是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
 如图,点D在△ABC的边AC上,添加下列一个条件仍不能判断△ADB与△ABC相似的是( )
如图,点D在△ABC的边AC上,添加下列一个条件仍不能判断△ADB与△ABC相似的是( )| A、∠ABD=∠C |
| B、∠ADB=∠ABC |
| C、BC2=CD•AC |
| D、AB2=AD•AC |
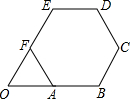 如图,正六边形ABCDEF的边长为2
如图,正六边形ABCDEF的边长为2 如图,直线AB,CD相交于点E,FE⊥AB,若∠FEC-∠AEC=20°,那么∠AED的度数是
如图,直线AB,CD相交于点E,FE⊥AB,若∠FEC-∠AEC=20°,那么∠AED的度数是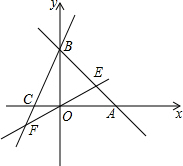 直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.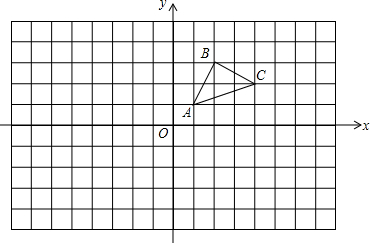
 a、b两数在一条隐去原点的数轴上的位置如图所示,①a-b<0;②a+b<0;③ab<0;④(a+1)(b+1)<0,上述4个式子中一定成立的是
a、b两数在一条隐去原点的数轴上的位置如图所示,①a-b<0;②a+b<0;③ab<0;④(a+1)(b+1)<0,上述4个式子中一定成立的是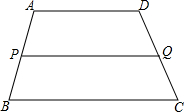 如图,在梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.
如图,在梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.