题目内容
3.七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的平行线相关性质进行了严格的证明,体会了数学的公理化化思想.请完成下列证明活动:活动1.利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)已知:如图1,直线AB、CD被直线EF所截,AB∥CD.
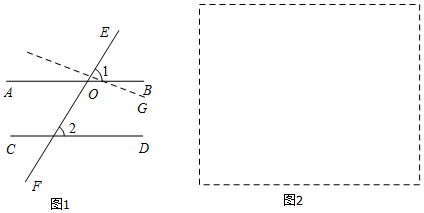
求证:∠1=∠2.
证明:假设∠1≠∠2,则可以过点O作∠EOG=∠2.
∵∠EOG=∠2,
∴OG∥CD(同位角相等,两直线平行).
∴过O点存在两条直线AB、OG两条直线与CD平行,这与基本事实(AB∥CD)矛盾.
∴假设不成立.
∴∠1=∠2.
活动2.利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程)
已知:AB∥CD.
求证:两直线平行,同旁内角互补.
证明:
分析 活动1,根据同位角相等,两直线平行可得出结论;
活动2,利用∠1=∠2,再由补角的定义即可得出结论.
解答  解:活动1,证明:假设∠1≠∠2,则可以过点O作∠EOG=∠2.
解:活动1,证明:假设∠1≠∠2,则可以过点O作∠EOG=∠2.
∵∠EOG=∠2,
∴OG∥CD(同位角相等,两直线平行).
∴过O点存在两条直线AB、OG两条直线与CD平行,这与基本事实(AB∥CD)矛盾.
∴假设不成立.
∴∠1=∠2.
故答案为:同位角相等,两直线平行,AB∥CD;
活动2,已知:AB∥CD,
求证:两直线平行,同旁内角互补.
证明:如图,∵AB∥CD,
∴∠1=∠2.
∵∠1+∠3=180°,
∴∠2+∠3=180°,即两直线平行,同旁内角互补.
故答案为:AB∥CD,两直线平行,同旁内角互补,
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.一组数据的方差为s2,将这组数据中的每一个数据都扩大到原来的3倍,所得的一组新数的方差是( )
| A. | $\frac{{s}^{2}}{9}$ | B. | 9s2 | C. | 3s2 | D. | s2 |
13. 如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )
如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )
 如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )
如图,直线l1、l2与直线l3相交,若l1∥l2,∠1=120°,则∠2=( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
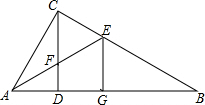 在△ABC中,∠ACB=90°,CD是斜边AB上的高,AE是∠CAB的交平分线,AE分别交CD、BC于点F、E,过点E作EG⊥AB于点G.
在△ABC中,∠ACB=90°,CD是斜边AB上的高,AE是∠CAB的交平分线,AE分别交CD、BC于点F、E,过点E作EG⊥AB于点G.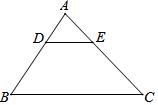 已知:如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=2,AB=6,求DE:BC的值.
已知:如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=2,AB=6,求DE:BC的值.