题目内容
11.将抛物线y=-$\frac{1}{2}$(x+1)2-2沿直线y=x方向向右上方平移2$\sqrt{2}$个单位,得到新抛物线的解析式为y=-$\frac{1}{2}$(x-1)2或y=-$\frac{1}{2}$(x+3)2-4.分析 根据等腰直角三角形的性质求出沿直线y=x的方向平移2$\sqrt{2}$个单位的横坐标与纵坐标的变化情况,然后分两种情况写出平移后的抛物线的顶点坐标,再利用顶点式解析式写出即可.
解答 解:∵沿直线y=x的方向平移2$\sqrt{2}$个单位,
∴横坐标和纵坐标都平移2个单位,
∵函数y=-$\frac{1}{2}$(x+1)2-2的顶点坐标为(-1,-2),
∴平移后的抛物线的顶点坐标为(1,0)或(-3,-4),
∴函数解析式为y=-$\frac{1}{2}$(x-1)2或y=-$\frac{1}{2}$(x+3)2-4.
故答案为:y=-$\frac{1}{2}$(x-1)2或y=-$\frac{1}{2}$(x+3)2-4.
点评 本题考查了二次函数图象与几何变换,此类题目,利用顶点的变化确定函数图象的变化更加简便.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
2.二次函数y=a(x+k)2+k,无论k为何实数,其图象的顶点都在( )
| A. | 直线y=x上 | B. | 直线y=-x上 | C. | x轴上 | D. | y轴上 |
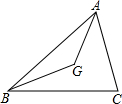 已知G点为△ABC的重心,S△ABG=1,求S△ABC=3.
已知G点为△ABC的重心,S△ABG=1,求S△ABC=3.