题目内容
5.设直线y=-2与抛物线y=ax2交于两点A、B,已知AB=6,求a的值.分析 由二次函数的对称性可知:直线y=-2与抛物线y=ax2交于两点A、B是关于y轴对称的,求得两点,利用求两点之间的距离计算方法列出方程求得a的数值即可.
解答 解:∵直线y=-2与抛物线y=ax2交于两点A、B,
∴ax2=-2,
∴x=±$\sqrt{\frac{-2}{a}}$,
∵AB=6,
∴$\sqrt{\frac{-2}{a}}$+$\sqrt{\frac{-2}{a}}$=6,
解得a=-$\frac{2}{9}$.
点评 此题考查二次函数的性质,掌握二次函数图象上点的坐标特征以及对称性是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
13.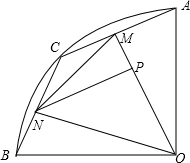 如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )
如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )
 如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )
如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )| A. | 随C点的运动而变化,NP的取值范围是1≤NP≤$\sqrt{2}$ | |
| B. | 随C点的运动而变化,最大值为$\frac{3\sqrt{2}}{2}$ | |
| C. | 等于$\sqrt{2}$ | |
| D. | 随C点的运动而变化,没有最值 |
10. 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则△ABC的面积是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则△ABC的面积是( )
 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则△ABC的面积是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则△ABC的面积是( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
14.在?ABCD中,已知∠A:∠B=1:3,则∠B的度数是( )
| A. | 135° | B. | 120° | C. | 90° | D. | 45° |
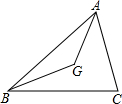 已知G点为△ABC的重心,S△ABG=1,求S△ABC=3.
已知G点为△ABC的重心,S△ABG=1,求S△ABC=3.