题目内容
6.计算:(1)一个等腰三角形的一边长为8cm,周长为20cm,求其它两边的长.
(2)已知等腰三角形的一边长等于6cm,一边长等于7cm,求它的周长.
(3)已知等腰三角形的一边长等于5cm,一边长等于12cm,求它的周长.
分析 (1)已知条件中,本题没有明确说明已知的边长是否是腰长,所以有两种情况讨论,还应判定能否组成三角形;
(2)分6是等腰三角形的腰长与底边两种情况讨论求解;
(3)题目给出等腰三角形有两条边长为5cm和12cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解答 解:(1)①底边长为8,则腰长为:(20-8)÷2=6,所以另两边的长为6cm,6cm,能构成三角形;
②腰长为8,则底边长为:20-8×2=4,底边长为8cm,另一个腰长为4cm,能构成三角形.
因此另两边长为8cm、4cm或6cm、6cm;
(2)①6是腰长时,周长=6+6+7=19;
②6是底边时,7是腰,周长=6+7+7=20;
综上,它的周长为19或20;
(3)分两种情况:
当腰为5cm时,5+5<12,所以不能构成三角形;
当腰为12cm时,12+12>5,12-12<5,所以能构成三角形,周长是:12+12+5=29cm.
点评 考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
16.某地区人口状况相对稳定,人寿保险公司根据多年统计综合,有一张关于该地区人口寿命的表格,现摘录部分内容如下.
根据上表解答下列各题:
(1)该地区达到50岁的人中,不能达到51岁的概率约是多少?能达到80岁的概率约为多少?(精确到0.001)
(2)如果有20000个50岁的人参加人寿保险,当年死亡的赔偿金均为10万元,预计保险公司需付这一项赔偿的总额为多少?
| 年龄 | 到达该年龄的人数 | 在该年龄死亡的人数 |
| 40 | 80500 | 892 |
| 50 | 78009 | 951 |
| 60 | 69891 | 1200 |
| 70 | 45502 | 2199 |
| 80 | 16078 | 2001 |
| … | … | … |
(1)该地区达到50岁的人中,不能达到51岁的概率约是多少?能达到80岁的概率约为多少?(精确到0.001)
(2)如果有20000个50岁的人参加人寿保险,当年死亡的赔偿金均为10万元,预计保险公司需付这一项赔偿的总额为多少?
 如图,已知$\frac{DB}{AD}=\frac{EC}{AE}$,AD=15,AB=40,AC=28,求AE.
如图,已知$\frac{DB}{AD}=\frac{EC}{AE}$,AD=15,AB=40,AC=28,求AE. 如图,△ABD≌△CDB,若AB=4,AD=5,BD=6,∠ABD=30°,则CD=4.
如图,△ABD≌△CDB,若AB=4,AD=5,BD=6,∠ABD=30°,则CD=4.



 已知数轴:A点表示0,B点表示2,C点表示-1.5.
已知数轴:A点表示0,B点表示2,C点表示-1.5.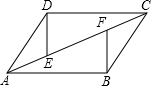 如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,试说明DE与BF的关系.
如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,试说明DE与BF的关系.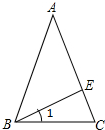 已知:如图,在△ABC中,AB=AC,∠1=$\frac{1}{2}$∠BAC,求证:BE⊥AC.
已知:如图,在△ABC中,AB=AC,∠1=$\frac{1}{2}$∠BAC,求证:BE⊥AC.