题目内容
12.已知方程组$\left\{\begin{array}{l}{3x+y=k+1,①}\\{x+3y=3,②}\end{array}\right.$试根据下列条件,求k的取值范围.(1)方程组的解x,y满足0<x+y<1
(2)方程组的解x,y满足x>0,y>0.
分析 (1)先利用加减消元法解方程组求出x、y,然后根据0<x+y<1列出不等式组,再解不等式组即可;
(2)先利用加减消元法解方程组求出x、y,然后根据x、y都是正数列出不等式组,再解不等式组即可.
解答 解:方程组$\left\{\begin{array}{l}{3x+y=k+1,①}\\{x+3y=3,②}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{3k}{8}}\\{y=\frac{8-k}{8}}\end{array}\right.$,
(1)当0<x+y<1时,即0<$\frac{k+4}{4}$<1,
∴-4<k<0,
(2)当x>0,y>0时,即$\left\{\begin{array}{l}{\frac{3k}{8}>0}\\{\frac{8-k}{8}>0}\end{array}\right.$,
∴$\frac{8}{3}$<k<8.
点评 本题考查了二元一次方程组的解,一元一次不等式的解法,用k表示出x、y是解题的关键,也是本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列图案可以看作某一部分平移后得到的是( )
| A. |  | B. |  | C. |  | D. |  |
17. 如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则$\frac{AM}{MD}$等于( )
如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则$\frac{AM}{MD}$等于( )
 如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则$\frac{AM}{MD}$等于( )
如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则$\frac{AM}{MD}$等于( )| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
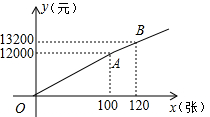 在体育局的策划下,市体育局将组织明星篮球队,为此体育局推出两种购票方案(设购票张数为x,购票总价为y).
在体育局的策划下,市体育局将组织明星篮球队,为此体育局推出两种购票方案(设购票张数为x,购票总价为y).