题目内容
16.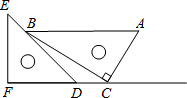 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=2,则CD的长为3-$\sqrt{3}$.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=2,则CD的长为3-$\sqrt{3}$.
分析 作BM⊥CF于M,则∠BMD=90°,由勾股定理得出BC=$\sqrt{3}$AC=2$\sqrt{3}$,由平行线的性质得出∠BCM=∠ABC=30°,由含30°角的直角三角形的性质得出MB=$\frac{1}{2}$BC=$\sqrt{3}$,求出MC=3,再证明△BMD是等腰直角三角形,得出DM=MB=$\sqrt{3}$,CD=MC-DM,即可得出结果.
解答 解:作BM⊥CF于M,如图所示: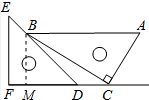
则∠BMD=90°,
∵∠ACB=90°,∠A=60°,
∴∠ABC=30°,
∴BC=$\sqrt{3}$AC=2$\sqrt{3}$,
∵AB∥CF,
∴∠BCM=∠ABC=30°,
∴MB=$\frac{1}{2}$BC=$\sqrt{3}$,
∴MC=$\sqrt{3}$BM=3,
∵∠F=90°,∠E=45°,
∴∠EDF=45°,
∴△BMD是等腰直角三角形,
∴DM=MB=$\sqrt{3}$,
∴CD=MC-DM=3-$\sqrt{3}$;
故答案为:3-$\sqrt{3}$.
点评 本题考查了勾股定理、平行线的性质、等腰直角三角形的判定与性质、含30°角的直角三角形的性质、三角函数等知识;本题综合性强,难度适中.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
4.受中日钓鱼岛事件的影响,在钓鱼岛被“国有化”的2012年9月份,某日本品牌食用油价格开始回落,食用油批发商批发这种品牌的食用油,每桶在9月份前四周每周的平均销售价格变化如下表:
进入10月份后,由于受中日关系趋于缓和等因素的影响,食用油的价格开始回升,该品牌食用油销售价格y2(元/桶)从10月份第1周的54元/桶,上升至第2周的57元/桶,且销售价格y2(元/桶)与周数x(x为整数)的变化情况满足二次函数:y2=-$\frac{1}{4}$x2+bx+c.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出9月份y1与x的函数关系式;并求出10月份y2与x的函数关系式.
(2)若9月份该品牌的食用油进价m1(元/桶)与周数x满足函数关系为:m1=$\frac{1}{3}$x2-3x+50,10月份该品牌的食用油进价m2(元/桶)与周数x满足函数关系为:m2=$\frac{7}{2}$x+$\frac{81}{2}$,试问在9月份和10月份中,哪月的哪一周销售一桶该品牌的食用油利润最大?最大利润是多少?
(3)在第(2)问的条件下,该批发商在10月份的第2周以该周的进价购入该品牌食用油1200桶,准备在10月份第3周进行销售.在第3周以该周的销售价销售了a%后,为了加快销售的进度,该批发商决定在原销售价格的基础上每桶降价4元进行销售,这样顺利地完成了第三周销售1200桶的任务,且获利12000元,算出a的值.
| 周数x | 1 | 2 | 3 | 4 |
| 价格y1(元/桶) | 60 | 59 | 58 | 57 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出9月份y1与x的函数关系式;并求出10月份y2与x的函数关系式.
(2)若9月份该品牌的食用油进价m1(元/桶)与周数x满足函数关系为:m1=$\frac{1}{3}$x2-3x+50,10月份该品牌的食用油进价m2(元/桶)与周数x满足函数关系为:m2=$\frac{7}{2}$x+$\frac{81}{2}$,试问在9月份和10月份中,哪月的哪一周销售一桶该品牌的食用油利润最大?最大利润是多少?
(3)在第(2)问的条件下,该批发商在10月份的第2周以该周的进价购入该品牌食用油1200桶,准备在10月份第3周进行销售.在第3周以该周的销售价销售了a%后,为了加快销售的进度,该批发商决定在原销售价格的基础上每桶降价4元进行销售,这样顺利地完成了第三周销售1200桶的任务,且获利12000元,算出a的值.
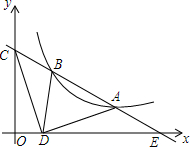 如图,已知反比例函数y=$\frac{m}{x}$与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与x轴、y轴的交点分别为C、E.
如图,已知反比例函数y=$\frac{m}{x}$与一次函数y=kx+b的图象相交于A(4,1)、B(a,2)两点,一次函数的图象与x轴、y轴的交点分别为C、E. 梯形ABCD中,DC∥AB,BC=10,且MN∥PQ∥AB,DM=MP=2PA,则CN=4,BQ=2.
梯形ABCD中,DC∥AB,BC=10,且MN∥PQ∥AB,DM=MP=2PA,则CN=4,BQ=2.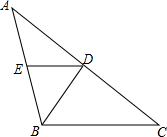 如图,在△ABC中,AB=BC,BD是∠ABC的平分线,DE∥BC.
如图,在△ABC中,AB=BC,BD是∠ABC的平分线,DE∥BC. 在△ABC中,DE∥BC交AB于D,交AC于E,且AD:DB=2:3,△ABC的周长为27cm,求△ADE的周长.
在△ABC中,DE∥BC交AB于D,交AC于E,且AD:DB=2:3,△ABC的周长为27cm,求△ADE的周长. 如图,△ABC中,∠B=30°,∠C=45°,AB=2$\sqrt{3}$,点E在边AB上,点D在边BC上,且满足∠AED=∠C,连接AD,若∠ADE=∠BAC.给出下列结论:①AD=BD;②AE=CD;③△BDE∽△ADB;④$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{3}$.其中正确的结论有①②④(把所有正确结论序号都填在横线上)
如图,△ABC中,∠B=30°,∠C=45°,AB=2$\sqrt{3}$,点E在边AB上,点D在边BC上,且满足∠AED=∠C,连接AD,若∠ADE=∠BAC.给出下列结论:①AD=BD;②AE=CD;③△BDE∽△ADB;④$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{3}$.其中正确的结论有①②④(把所有正确结论序号都填在横线上)